
The world’s tallest protein skimmer? This venturi-driven prototype was designed and built by the author using techniques described in this 2-part article. At 17 feet tall, I believe it to be the tallest skimmer around (the RK2000PE skimmer stands 14.25′). Note that about 10 feet of the skimmer is in a concrete pit. If you know of a taller skimmer, please send me a photo. I can be reached at [email protected].
I am often faced with a situation where a specialized piece of equipment is needed and either it is available commercially and exceeds my budget, or it simply does not exist and must be custom built. To compound the situation, I am on a virtual outpost in the middle of the Pacific Ocean, where specialized equipment such as lathes or small machining tools are not readily available, or available through mail-order but with shipping charges that can easily double the price seen on the mainland U.S. In short, I must make do with limited resources and manufacture many of the devices used in research experiments, and in this article I will share some of my ‘secrets’. Most of this work can be done using a minimum of tools, although having access to certain equipment will be of great use in expediting the project. If you’re a homeowner, you probably have many of the ‘luxury’ tools in your garage (or your neighbors have them in theirs’). Instead of describing
the method of designing and building a specific project, we’ll examine manufacturing techniques that are applicable to a wide variety of jobs.
Before continuing, just a word of caution. Building various devices can often save you some money, but this is not guaranteed. I have tackled a number of projects where the end result needed some ‘tweaking’ – so much so, that I eventually scrapped the prototype and built a second unit. When it was all said and done, and I considered the amount of my time and money invested, I realized that it would have been a lot less hassle and probably less expensive to buy a commercially available unit.
Secondly, not everyone is handy with tools. Many hand and/or power tools are a hazard to an inexperienced user, and we often work with materials than can readily slice or cut hands and fingers. The old adage about having blood, sweat and tears in a project is based on many experiences! Make sure you follow all safety precautions with any hand or power tools you use!
However, careful workers taking their time and avoiding the temptation to rush a job to completion can produce quality products safely. Before attempting any job, make an honest assessment of your skills and resources.
If you’re still with me, you’ve decided to take the plunge and learn some valuable techniques. We’ll start with:
Planning Your Work
Planning your work is the most important part of a successful project and the saying ‘Failure to plan is a plan for failure’ is certainly true. At a very minimum, I sketch out the design on paper and then sleep on the idea. Usually, I’ll re-draw the design several times before actually beginning construction. Don’t rush this part of the project.
If you’re really into getting the fine details worked out, see these two articles by Shane Graber where he describes using a computer and free shareware in the ultimate in design layout:
Once you’ve gathered your parts, it is best to place them together in a ‘dry run’ to fully visualize your plan. You’ll likely find that slight modifications need to be made in order for everything to fit together perfectly.
Warning: Never plumb a drinking water (also called potable water) line directly into a reactor or below the water line of a water-containing vessel unless a suitable back flow preventer is installed. Even better, use an air gap between the discharge of the potable water line and the reservoir (the air gap distance should be about 5 times the diameter of the pipe). Failure to use some sort of backflow prevention could result in your house’s drinking water system becoming contaminated.
Conversion of Fractions to Decimals
Table 1 offers a reference listing conversions of fractions to decimals. As most of you know, fractions must be converted to decimals when adding, subtracting, multiplying or dividing, and this is important when calculating area, volume, flow, etc. More on calculating areas and volumes later in this article.
| Fraction | Decimal | Fraction | Decimal |
|---|---|---|---|
| 1/64″ | 0.015625 | 33/64″ | 0.515625 |
| 1/32″ | 0.03125 | 17/32″ | 0.53125 |
| 3/64″ | 0.046875 | 35/64″ | 0.546875 |
| 1/16″ | 0.0625 | 9/16″ | 0.5625 |
| 5/64″ | 0.078125 | 37/64″ | 0.578125 |
| 3/32″ | 0.09375 | 19/32″ | 0.59375 |
| 7/64″ | 0.109375 | 38/64″ | 0.609375 |
| 1/8″ | 0.125 | 5/8″ | 0.625 |
| 9/64″ | 0.140625 | 41/64″ | 0.640625 |
| 5/32″ | 0.15625 | 21/32″ | 0.65625 |
| 11/64″ | 0.171875 | 43/64″ | 0.671875 |
| 3/16″ | 0.1875 | 11/16″ | 0.6875 |
| 13/64″ | 0.203125 | 45/64″ | 0.703125 |
| 7/32″ | 0.21875 | 23/32″ | 0.71875 |
| 15/64″ | 0.234375 | 47/64″ | 0.734375 |
| 1/4″ | 0.25 | 3/4″ | 0.75 |
| 17/64″ | 0.265625 | 49/64″ | 0.765625 |
| 9/32″ | 0.28125 | 25/32″ | 0.78125 |
| 19/64″ | 0.296875 | 51/64″ | 0.796875 |
| 5/16″ | 0.3125 | 13/16″ | 0.8125 |
| 21/64″ | 0.328125 | 53/64″ | 0.828125 |
| 11/32″ | 0.34375 | 27/32″ | 0.84375 |
| 23/64″ | 0.359375 | 55/64″ | 0.859375 |
| 3/8″ | 0.375 | 7/8″ | 0.875 |
| 25/64″ | 0.390625 | 57/64″ | 0.890625 |
| 13/32″ | 0.40625 | 29/32″ | 0.90625 |
| 27/64″ | 0.421875 | 59/64″ | 0.921875 |
| 7/16″ | 0.4375 | 15/16″ | 0.9375 |
| 29/64″ | 0.453125 | 61/64″ | 0.953125 |
| 15/32″ | 0.46875 | 31/32″ | 0.96875 |
| 31/64″ | 0.484375 | 63/64″ | 0.984375 |
| 1/2″ | 0.5 | 1″ | 1 |
Determining Volume
You’ll sometimes want to know the volume of a device in order to size it correctly. Since most of these projects will be rather small in size, we can use these formulae.
To determine the volume of a square or rectangular tank (in gallons):
Length x Width x Depth (all in inches) divided by 231 = U.S. Gallons
Example: A rectangular tank is 24 inches long, 12 inches wide and 12 inches deep. What is the volume?
Answer: 24 x 12 x 12 = 3,456 cubic inches. 3,456 divided by 231 (the number of cubic inches in a U.S. Gallon) = 14.96 U.S. Gallons
To determine the volume of a cylindrical tank (in gallons):
Measure diameter then divide by 2 to obtain the radius. Then use the formula:
volume = πr2
Where π = 3.14
Example: A tube or cylinder is 4 inches in diameter and is 12 inches long (or deep). How many gallons does it hold?
Answer: 1. Determine the radius: Diameter divided by 2 = radius; 4 inches in diameter divided by 2 = Radius of 2 inches. Multiply radius by 3.14 (which is pi, or ): 2 x 3.14 = 6.28. How multiply the area of the cylinder by the length (or depth) to determine volume in cubic inches: 6.28 x 12 = 75.36 cubic inches. Now, divide volume by 231 to determine U.S. gallons: 75.36 divided by 231 = 0.326 gallons. If you want this in ounces, do this: 0.326 x 128 ounces per U.S. Gallon = ~42 ounces.
Example: You want to build a reactor that will house 1 quart of media (GAC, phosphorus removal material, etc.) and have a piece of 2″ PVC pipe. Barb fittings at the top and bottom will add another 3 inches to the height. It must fit into an aquarium stand that has 34 inches of ‘usable’ height. How tall will the reactor be if it holds the entire quart, and will it fit into the stand?
Answer: 1 quart = ¼ gallon, so 231 cubic inches divided by 4 = ~58 cubic inches. Each inch of length of 2″ pipe holds about 3.14 cubic inches (use r², hence: 1*1*3.14 = 3.14 cubic inches). Divide volume of media (58) by volume of pipe per inch (3.14).
The answer is about 18.5″ in height. The reactor will fit even if it is made 20″ tall and still allows room for the installation of the barb fittings.
Avoid the temptation to think that doubling the pipe diameter merely doubles its area! It does not – it quadruples it! If you have any doubts, use the formula above on a 1″ and 2″ pipe, for instance.

Figure 3. Circumference of OD minus ID equals the length of the material that must be cut away to equal a perfect ‘internal’ fit. A carefully measured and cut friction fit sleeve can be surprisingly water-tight.
Circumference
If you built a lot of equipment, you’ll occasionally need to figure circumference. The formula is simple:
circumference = πd, or 3.14 times diameter.
You’ll need to know this for various reasons, but I’ve used it most often to fashion a ‘stop’ or beef up the ID of a tube or pipe (this is handy when building protein skimmers).
Calculating the Volume of a Cone
I mention this calculation mostly for those wishing to build their own protein skimmer (plastic funnels make a perfect transition from the air reaction chamber to the chimney where the gunk is separated from the water. In any case, this calculation is straightforward – measure the diameter of the top (widest) part of the funnel and then the height. Calculate the volume as you would for a cylinder of this diameter and height, and then divide by 3. That’s it – simple!

Figure 4. Calculating the total volume of this funnel would require figuring the volume of two cones.
Pumps
Reef aquaria would be practically impossible to maintain without pumps. They provide flow, circulation, recirculation, and allow protein skimmers and chemical reactors to operate properly. Pumps, being the mechanical devices they are, have special names for their parts and operational parameters. Before being our discussion of pumps, we’ll review some of the terminology.
Pump Terminology
- Cavitation:
- Cavitation is a phenomenon where the intake of a pump is restricted or the liquid is somehow restricted causingthe impeller to create an area of low pressure. This results in water boiling and the violent formation, followed by collapse, of tiny air bubbles (yes, under low pressure, water can boil at the operating temperatures of reef aquaria!). These bubbles ‘sandblast’ an impeller and can destroy it overtime. Cavitation of large pumps is accompanied by a low rumbling noise, but is unlikely to be heard on most pumps used in aquaria. Cavitation should not be confused with those pumps designed to shred air (such as needle wheel impellers) or a pump that is pulling air through the intake.
These lesson here – Do not reduce the intake piping size of a centrifugal pump!
- Dead Head:
- Jerry Garcia fans unite! Seriously, ‘dead head’ is a legitimate engineering term. It simply refers to pumps’ abilities to avoid destruction if a discharge isolation valve is closed. Centrifugal pumps can generally operate against a closed discharge for at least short periods of time without suffering damage. On the other hand, positive displacement pumps (such a peristaltic, piston, or diaphragm pumps) can not survive for long similar operations – something will have to give as pressure rises. It is usually a discharge line, hose or diaphragm, sometimes with explosive force.
- Flooded Suction:
- As the name implies, this situation is observed when the pump is situated below the water line of a tank. This is often seen with centrifugal pumps that are not self-priming.
- Flow:
- The volume of fluid that passes through a passage of a given area in a given amount of time.
- Friction Loss:
- Water ‘rubs’ against even the smoothest of pipes and results in pressure losses due to friction. There is friction loss even in short runs of pipe, although the effect may be negligible. A good example of friction loss can be seen in small glass or plastic tubes (such as those the size of airline tubing). Water can get trapped within the tubing, even when held vertically, since the small amount of water is not of sufficient weight to overcome the pipe wall friction, and must be blown out.
- Head:
- The vertical lift that a pump must push against. Head is usually reported in feet, and is the sum of friction loss within the length (or height) of the pipe, the number of fittings and their impedance to flow, specific gravity of the liquid being pumped, and so on. Head (or vertical lift) is seldom reported in pounds per square inch.
- Impeller:
- A disk with vanes that spins and propels liquids. The impeller is contained in a chamber called a volute.
- Pressure:
- Exertion of force upon a surface by a liquid in contact with it.
- Prime:
- To fill the volute with water in order for the pump to start pumping. Some pumps are self-priming.
- Specific Gravity:
- The ratio of density of a liquid to the density of pure water. Seawater is ~1.025 more dense than pure water.
- Suction Head:
- When the pump must pull a liquid upwards (such as the case with peristaltic or metering pumps) the friction of the intake line and fittings must be considered, and is called Suction Head.
- Suction Lift:
- Suction lift exists when a pump is above the water line of a non-pressurized tank. Obviously, the pump must be self-priming to work in this situation.
- Volute:
- The housing containing the impeller or propeller. Volutes have an intake and discharge. The size of the intake and discharge are engineered according to the amount of rated flow, and it is not a good idea to reduce the size of the recommended pipe on either.
Types of Pumps
There are a number of pumps available to hobbyists that are ‘aquarium safe’. It is important to choose the right pump for the application. The following will give some tips on selection.

Figure 5. A fractional horsepower centrifugal pump called a powerhead. These are excellent for moving moderate amounts of water.
Centrifugal Pumps
Centrifugal pumps are perhaps the most common pumps seen in the aquarium industry. A propelling force created by a vaned disk (the impeller, which is driven by an electrical motor) rotates rapidly with a chamber (the volute). This energy propels the fluid through the pump and onwards to the discharge.
Magnetic drive pumps are generally preferred to mechanically-coupled pumps. As the name implies, a spinning drive by the electrical motor is magnetically coupled to the impeller within the volute. There is no direct contact between these magnets, and this eliminates the need for mechanical seals (that are required for direct-drive pumps). This makes for a reliable pump since mechanical seals will leak if the pump ever runs dry for an extended period of time.
Centrifugal pumps can be submersible, in-line on the dry-side of a sump, or sometimes both.
Magnetic Drive Centrifugal Pumps (External)
- Self-Priming: No, Use Flooded Suction
- Volume: High
- Pressure: Low
These are popular types of centrifugal pumps and for good reason. A ceramic magnetic and impeller (inert in seawater) is driven by an isolated motor forcing water through a plastic volute and discharge. Also called mag-drive pumps.
Since these pumps are external, they usually add very little heat to the aquarium. They should be plumbed with union ball valves on the intake and discharge sides to make servicing or replacement easier. Do not run these pumps dry.
Magnetic Drive Centrifugal Pumps (Internal, or Submersible)
- Self-Priming: Yes
- Volume: High
- Pressure: Low
These offer advantages such as ease of installation and removal and simple plumbing. Most submersibles are fractional horsepower pumps but can transfer a considerable amount heat to the water. Do not run these pumps dry.
Straight Drive Centrifugal Pumps
- Self-Priming: No, Use Flooded Suction
- Volume: High
- Pressure: Low
Similar to magnetic drive centrifugal pumps, except that the impeller is driven by the motor’s shaft. A mechanical seal (or rarely, packing) prevents leakage where the shaft penetrates the volute. These require more maintenance than a mag-drive, due to periodic replacement of the packing or, if the pump has run dry for an extended period, the mechanical seal.

Figure 6. An impeller (left) and a propeller (right). Both are utilized in aquarium water pumps and have preferred applications.
Propeller Pumps
- Self-Priming: Yes
- Volume: High
- Pressure: Very Low
Propeller pumps are a modification of the magnetic drive pump, where a propeller replaces the impeller. Generally, these pumps are very good at moving large amounts of water, but produce relatively little discharge pressure, hence they are recommended for low-head situations such as circulation within an aquarium.
Positive Displacement Pumps
Positive Displacement Pumps are usually found in use for aquaria as metering pumps, or applications where high pressure is required. Diaphragm and Peristaltic Pumps are common; Gear Pumps less so. Piston pumps could be used to provide a wave-like surge in aquarium, although I have never personally seen such an application.
Warning: Never block the discharge from a positive displacement pump (such as with a ball or globe valve) when the pump is running! Explosive pump or line failure will result!

Figure 7. Two peristaltic pumps in an industrial setting. These are very effective in delivering exact doses of chemical, and do so with little maintenance.
Peristaltic Pumps
- Self-Priming: Yes (usually limited to suction head of 15 feet or so)
- Volume: Low
- Pressure: Moderate to High
Peristaltic Pumps, sometimes called Hose Pumps, are positive displacement pumps using revolving rollers to ‘pinch’ a liquid-filled hose thereby ‘pushing’ the liquid through the discharge. Hose pumps are exceptionally good at moving abrasive materials (since it is the hose that wears) but are usually used in aquaria as metering pumps where a steady, relatively low volume delivery is required. They are generally long-lived, and routine maintenance includes replacing the peristaltic hose (easily done in a few minutes). These pumps are self-priming.
The amount of flow can be adjusted on some peristaltic pumps by varying the speed of a DC motor. Others have variously sized cartridges that allow use of larger tubing sizes.
Metering (Diaphragm) Pump
- Self-Priming: Yes, but usually limited to suction head of 4 feet or so.
- Volume: Low
- Pressure: Moderate to High
Diaphragm pumps are another sort of positive displacement pump. They are usually relatively low volume pumps but can produce high pressure on the discharge side. Like the peristaltic pump, these are useful where small yet precise volumes of water are pumped.
Metering pumps have some drawbacks. Their operation is inherently noisy, where a rhythmic ‘knock-knock-knock’ is produced by the motor/pulsing diaphragm/internal check balls. Diaphragms do not last forever, and the pump will require a periodic rebuild. This involves disassembly of the wet side of the pump and handling small springs and ceramic check balls. Invariably, one of these parts manages to escape the mechanic. Perhaps this overstates the frustration I’ve experienced with diaphragm pumps – the rebuild is not particularly difficult or time consuming.
Metering pumps are available in several models. The least expensive will deliver a preset volume and allows for no adjustment. Other models offer flow adjustments through either speed of the pump (strokes per minute) or volumetric adjustment (volume delivered by each stroke of the pump). The most expensive models have adjustments for both pump speed and stroke.
Gear Pumps
- Self-Priming: Yes
- Volume: High
- Pressure: High

Figure 9. Terminology used in reference to self-priming pumps (in aquaria, this generally includes only peristaltic and metering pumps).
Gear pumps use gears with closely machined tolerances in a housing with similar close tolerances. The pumped liquid is forced by the gears at relatively high pressure. Like centrifugal pumps, the flow is seamless and without major pulsation. These pumps are not usually seen in aquaria applications.
Piston Pumps
- Self-Priming: Yes, with flooded suction.
- Volume: Usually High
- Pressure: High
These pumps can pump either air or water, although I have never seen a piston pump used to pump water in a home aquarium. I recall having a piston-type air pump about 20 years ago, but these are rarely seen now.

Figure 10. Terminology used with flooded suction pumps (including almost all centrifugal pumps used in home aquaria).
Piston pumps work much like the piston in an internal combustion engine. A down-stroke pulls air into the cylinder and an upstroke ‘pushes’ water or air out of the cylinder through a simple check ball valve.
Sizing Your Pump
Before beginning many projects, you’ll need to determine the flow rate needed for your particular project. These are various ways to determine this. Some involve this formula:
Perhaps the better way to determine pump size is to use a Pump Curve.
Pump Curves graphically illustrate a pump’s pumping capacities under various circumstances. See Figure 11. In order to know the pump size and/or flow rate, you’ll need to know how ‘hard’ the pump must push the water. The resistance to flow is called ‘head’. You’ll refer to several Tables (below) to get the data to determine head. One thing you already know is the Specific Gravity of the liquid (Freshwater = 1.0; Saltwater = 1.025, and brackish is somewhere in between). Next you’ll need to determine the size of the pipe work, approximate flow rate (yeah, I know. That’s what we’re trying to determine, so make an educated guess – See Table 6), the number and size of the fittings (90 degree bends, etc.). If the manufacturer recommends the size of the discharge pipe, they have probably calculated friction loss caused by the pipe into the pump curve.
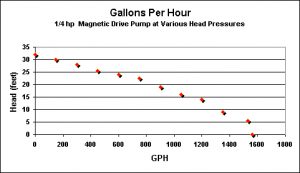
Figure 11. A Pump Curve from an Iwaki magnetic drive centrifugal pump. Determine the feet of head (y-axis) and find the intersection on the x-axis. Example: At 25 feet of head, this pump will deliver about 430 US gallons per hour.
Friction Loss
Water rubs the side of the pipe as it moves. Larger amounts of flow result in more friction and pipe diameter also plays an important part. Friction ‘burns up’ the rated head of a pump. While the friction loss is minimal with short runs of pipe, excessive head loss can result from too much discharge piping, excessive number of bends, etc.
The age of the pipe also should be considered. PVC and other plastic piping becomes coated with various things including calcium deposits, biological slimes and bio-growths. All cause addition friction. Tables 2 and 3 list friction losses (head losses) for older ‘in-use’ pipe and new pipe.
| Flow (GPH) | Pipe Diameter (ID – Inches) | ||||||
|---|---|---|---|---|---|---|---|
| 1/2″ | 3/4″ | 1″ | 1-1/4″ | 1-1/2″ | 2″ | 2-1/2″ | |
| 30 | 0.11 | 0.01 | |||||
| 60 | 0.38 | 0.05 | 0.01 | ||||
| 120 | 1.37 | 0.19 | 0.05 | 0.02 | 0.01 | ||
| 180 | 2.9 | 0.4 | 0.1 | 0.03 | 0.01 | ||
| 240 | 4.93 | 0.68 | 0.17 | 0.06 | 0.02 | 0.01 | |
| 300 | 7.45 | 1.03 | 0.25 | 0.09 | 0.04 | 0.01 | |
| 600 | 3.73 | 0.92 | 0.31 | 0.13 | 0.03 | 0.01 | |
| 900 | 7.9 | 1.95 | 0.66 | 0.27 | 0.07 | 0.02 | |
| 1200 | 3.31 | 1.12 | 0.46 | 0.11 | 0.04 | ||
| 1800 | 7.01 | 2.37 | 0.97 | 0.24 | 0.08 | ||
| 2400 | 4.03 | 1.66 | 0.41 | 0.14 | |||
| 3000 | 6.09 | 2.51 | 0.62 | 0.21 | |||
| Flow (GPH) | Pipe Diameter (ID – Inches) | ||||||
|---|---|---|---|---|---|---|---|
| 1/2″ | 3/4″ | 1″ | 1-1/4″ | 1-1/2″ | 2″ | 2-1/2″ | |
| 30 | 0.09 | 0.01 | |||||
| 60 | 0.33 | 0.05 | 0.01 | ||||
| 120 | 1.19 | 0.17 | 0.04 | 0.01 | 0.01 | ||
| 180 | 2.53 | 0.35 | 0.09 | 0.03 | 0.01 | ||
| 240 | 4.3 | 0.6 | 0.15 | 0.05 | 0.02 | 0.01 | |
| 300 | 6.5 | 0.9 | 0.22 | 0.07 | 0.03 | 0.01 | |
| 600 | 3.25 | 0.8 | 0.27 | 0.11 | 0.03 | 0.01 | |
| 900 | 6.89 | 1.7 | 0.57 | 0.24 | 0.06 | 0.02 | |
| 1200 | 2.89 | 0.97 | 0.4 | 0.1 | 0.03 | ||
| 1800 | 6.12 | 2.06 | 0.85 | 0.21 | 0.07 | ||
| 2400 | 3.51 | 1.45 | 0.36 | 0.12 | |||
| 3000 | 5.31 | 2.18 | 0.54 | 0.18 | |||

Figure 12. Threaded fittings have internal threads or external threads and are called female and male, respectively. Avoid their use if possible. Instead use ‘slip’ fittings (those without threads) if possible. See text for details.
Friction Loss Due to Fittings
Bends in pipe cause additional friction and can greatly reduce a pump’s potential discharge rate. Interestingly, threaded fittings create a good deal more friction than slip fittings. Ironically, threaded fittings are recommended for higher pressure systems. The take-home message: Avoid use of threaded fittings unless there is a compelling reason to do so. See Tables 4 and 5 for further information.
| Screwed Fittings | ½ | ¾ | 1 | 1-¼ | 1-½ | 2 | 2-½ | 3 | 4 |
|---|---|---|---|---|---|---|---|---|---|
| 90° (Regular) | 3.6 | 4.4 | 5.2 | 6.6 | 7.4 | 8.5 | 9.3 | 11 | 13 |
| 90° (Long Radius) | 2.2 | 2.3 | 2.7 | 3.2 | 3.4 | 3.6 | 3.8 | 4 | 4.6 |
| 45° | 0.7 | 0.9 | 1.3 | 1.7 | 2.1 | 2.7 | 3.2 | 4 | 5.5 |
| Globe Valve | 22 | 24 | 29 | 37 | 42 | 54 | 62 | 79 | 110 |
| Gate Valve | 0.6 | 0.7 | 0.8 | 1.1 | 1.2 | 1.5 | 1.7 | 1.9 | 2.5 |
| Strainer | 5 | 6.6 | 7.7 | 18 | 20 | 27 | 29 | 34 | 42 |
| Slip Fittings | ½ | ¾ | 1 | 1-¼ | 1-½ | 2 | 2-½ | 3 | 4 |
|---|---|---|---|---|---|---|---|---|---|
| 90° (Regular) | 0.9 | 1.2 | 1.6 | 2.1 | 2.4 | 3.1 | 3.6 | 4.4 | 5.9 |
| 90° (Long Radius) | 1.1 | 1.3 | 1.6 | 2 | 2.3 | 2.7 | 2.9 | 3.4 | 4.2 |
| 45° | 0.5 | 0.6 | 0.8 | 1.1 | 1.3 | 1.7 | 2 | 2.6 | 3.5 |
| Globe Valve | 38 | 40 | 45 | 54 | 59 | 70 | 77 | 94 | 120 |
Theoretical Detention Time
In many applications you’ll want to know how long water is in contact with media within a chamber, or the length of time water dwells within a protein skimmer. Water moving too fast through a chamber could result in too little contact time with media or bubbles. Water moving too slowly might be effectual in removing undesirable wastes, but the generation of these wastes within the aquarium could exceed the removal rate within the reactor.
Estimating the Detention Time is easy. Figure the amount of water the reactor can hold when it is full of media (easily done with a kitchen measuring cup or volumetric cylinder). The water volume of the reactor is then divided by the pump flow rate.
Example: A reactor holds two quarts of media, but checking the water volume by filling it to overflow with water from a measuring cup finds that the media displaces 1 quart, and therefore the reactor can hold 1 quart of water. A pump delivering 50 gallons per hour is used. What is the Detention Time?
Answer: Determine if you want the detention time in seconds or minutes.
If minutes: 50 gallons per hour equals 0.833 gallons per minute (or 3.33 quarts per minute). The reactor holds 1 quart of water, therefore 1 divided by 3.33 = 0.3 minutes theoretical detention time.
Of course, to convert to seconds, multiply 60 seconds per minute by 0.3 to arrive at a detention time of 18 seconds.
Is this sufficient contact time? Unfortunately there is no pat answer as every situation differs in reactor load rates, total system water volume and many, many more. However, 18 seconds seems low, so the options are to increase reactor size or decrease the flow rate through the reactor.
Useful Formulae
- 1 U.S. Gallon = 8.34 pounds (freshwater, seawater slightly more)
- 1 cubic foot = 7.48 U.S. gallons
- 1 cubic foot = 62.38 pounds
- Cubic inches per U.S. gallon: 231
- 1 foot of head = 2.31 psi
- Pounds per Square Inch = 0.434 x Head (feet) x Specific Gravity
- Velocity = Flow/Area
- Flow = Area x Velocity
How Much Flow?
Generally, water velocity within a pipe should not exceed 5 feet per second. For velocities in different pipe sizes at varying flow rates, see Table 6. In addition, if the pumped fluid has much detritus or other suspended solids, or there is a possibility that the pump could move sand or other such coarse material into the pipe, it is recommended that a velocity of at least 2 feet per second is maintained.
| GPH | Pipe Diameter (Inside) | |||||
|---|---|---|---|---|---|---|
| 1/2″ | 3/4″ | 1″ | 1.25″ | 1.5″ | 2″ | |
| 36 | 0.196178344 | 0.0871904 | 0.0490446 | 0.0313885 | 0.0217976 | 0.0122611 |
| 72 | 0.392356688 | 0.1743808 | 0.0980892 | 0.0627771 | 0.0435952 | 0.0245223 |
| 108 | 0.588535032 | 0.2615711 | 0.1471338 | 0.0941656 | 0.0653928 | 0.0367834 |
| 144 | 0.784713376 | 0.3487615 | 0.1961783 | 0.1255541 | 0.0871904 | 0.0490446 |
| 180 | 0.98089172 | 0.4359519 | 0.2452229 | 0.1569427 | 0.108988 | 0.0613057 |
| 216 | 1.177070064 | 0.5231423 | 0.2942675 | 0.1883312 | 0.1307856 | 0.0735669 |
| 252 | 1.373248408 | 0.6103326 | 0.3433121 | 0.2197197 | 0.1525832 | 0.085828 |
| 288 | 1.569426752 | 0.697523 | 0.3923567 | 0.2511083 | 0.1743808 | 0.0980892 |
| 324 | 1.765605096 | 0.7847134 | 0.4414013 | 0.2824968 | 0.1961783 | 0.1103503 |
| 360 | 1.961783439 | 0.8719038 | 0.4904459 | 0.3138854 | 0.2179759 | 0.1226115 |
| 720 | 3.923566879 | 1.7438075 | 0.9808917 | 0.6277707 | 0.4359519 | 0.2452229 |
| 1080 | 5.885350318 | 2.6157113 | 1.4713376 | 0.9416561 | 0.6539278 | 0.3678344 |
| 1440 | 7.847133758 | 3.487615 | 1.9617834 | 1.2555414 | 0.8719038 | 0.4904459 |
| 1800 | 9.808917197 | 4.3595188 | 2.4522293 | 1.5694268 | 1.0898797 | 0.6130573 |
| 2160 | 11.77070064 | 5.2314225 | 2.9426752 | 1.8833121 | 1.3078556 | 0.7356688 |
| 2520 | 13.73248408 | 6.1033263 | 3.433121 | 2.1971975 | 1.5258316 | 0.8582803 |
| 2880 | 15.69426752 | 6.97523 | 3.9235669 | 2.5110828 | 1.7438075 | 0.9808917 |
| 3240 | 17.65605096 | 7.8471338 | 4.4140127 | 2.8249682 | 1.9617834 | 1.1035032 |
| 3600 | 19.61783439 | 8.7190375 | 4.9044586 | 3.1388535 | 2.1797594 | 1.2261146 |
Flow Meters
Flow meters are generally of a couple of types: Mechanical and Electronic. Electronic flow meters are available to those with deep pockets – prices start at ~$200, but often are in the $500-$700 bracket. Many use a paddle wheel that spins in the flow and can be used to estimate gallons per minute and totalized flow. Others operate using the Faraday Law, where moving water distorts a magnetic field and can be converted to flow rates and these can cost several thousand dollars.
Mechanical flow meters are much less expensive. They consist of a hollow clear acrylic tube with a guide rod at the center of the tube. Riding upon this guide rod is a stainless steel indicator that is pushed upwards by water flow moving through the flow meter. The outside of the hollow acrylic tube is marked with hash marks indicating flow in various increments depending upon the intended use (such as standard cubic feet per minute -scfm – for air, or gallons per minute or liters per minute for liquids).

Figure 14. A flow meter for liquids. Notice the slight corrosion of the stainless steel rod and indicator. See comments below.

Figure 13. A direct-reading flow meter for air. Note that the air compressor used in this application is oiled-lubricated – avoid use of these compressors and utilize an oil-less compressor for aquaria.
Measuring Pressure on the Discharge of a Centrifugal Pump
If the intent is to merely monitor pump output, in lieu of a flow meter, consider installing a pressure gauge. These are available through well-stocked hardware stores. It is not terribly difficult to pump in a gauge on the discharge side of a centrifugal pump. Make sure the gauge is engineered for use with liquids and is corrosion-resistant. Better gauges are liquid-filled to dampen surges thus preventing damage to the device.
A Note about Stainless Steel
Stainless steel is available in various grades and the best is advertised to be inert in seawater. Even so, I have observed some degradation of stainless steel after prolonged exposure to seawater. The amount of metals added to a captive system’s water is likely quite small, but I would recommend regular water changes when stainless is used.
Personally, I try to minimize the use of stainless steel whenever possible. Use of plastic clamps is recommended over use of stainless worm clamps.
Minimum Tools
A surprising amount of work can be performed with a minimum of basic hand tools. Work may not proceed as quickly as when using power tools, but the end product can be of comparable quality. These tools are recommended:
- Tape measure (small, 10 foot is fine for our purposes)
- Hacksaw (cheapest possible)
- Glass Cutter (get one without a replaceable cutter – it is less expensive)
- Drill Motor and bits (battery or electric, variable speed, accepts ½” bits)
- Builders’ Square (plastic, inexpensive)
- Sharpie™ permanent markers (excellent for marking glass, plastics, and just about anything else).
Shop wisely and these tools can be acquired for about $40 U.S.
Eggcrate
If there was every a gift from the heavens to reef aquarists, it has to be eggcrate material. Intended for use as a parabolic reflector in fluorescent light panels, this material has seen an incredible number of applications in the aquarium hobby. The white plastic material is inert in seawater and therefore does not corrode or seem to leach any toxic materials into the water (the same is probably not true for the eggcrate with an applied reflective silver material). It is easily cut with a handsaw, jigsaw or linesman’s pliers. Eggcrate is available at any hardware store in the lighting section.
Note that all eggcrate is not created equal. Some eggcrate has thicker, tapered walls while other eggcrate has thin walls and is not tapered.
Glass Thickness
Water is some heavy stuff and its weight can cause glass to flex and break if the glass is too thin. Obviously this is an unwanted occurrence, and it is important to choose the proper glass thickness when building an aquarium or other device intended to hold water. Since the pressure on the aquarium bottom is dependent upon the depth of the water column and hence the weight of the water pressing against it, the bottom pane is usually made of thicker glass. The force of the water pushing against the sides is usually less, so thinner glass can be used.
| Height (Depth) | 24″ Length | 36″ Length | 48″ Length | 60″ Length | 72″ Length | 84″ Length | 96″ Length |
|---|---|---|---|---|---|---|---|
| 15 | 1/4″ | 1/4″ | 1/4″ | 1/4″ | 1/4″ | 1/4″ | 1/4″ |
| 18 | 1/4″ | 1/4″ | 1/4″ | 1/4″ | 1/4″ | 1/4″ | 1/4″ |
| 21 | 1/4″ | 1/4″ | 3/8″ | 3/8″ | 3/8″ | 3/8″ | 3/8″ |
| 24 | 1/4″ | 3/8″ | 3/8″ | 3/8″ | 3/8″ | 3/8″ | 3/8″ |
| 27 | 3/8″ | 1/2″ | 1/2″ | 1/2″ | 1/2″ | 1/2″ | 1/2″ |
| 30 | 3/8″ | 1/2″ | 1/2″ | 1/2″ | 1/2″ | 5/8″ | 5/8″ |
| 33 | 1/2″ | 1/2″ | 5/8″ | 5/8″ | 5/8″ | 5/8″ | 5/8″ |
| 36 | 1/2″ | 1/2″ | 5/8″ | 5/8″ | 5/8″ | 7/8″ | 7/8″ |
That does it for this month. The information presented in this installment should get you started in properly planning a project. Next month, we’ll look an in-depth look at PVC pipe and other fittings as well as techniques used to construct your project.






0 Comments