Let’s start with a simple observation: many of the organisms that live in the ocean and that we keep in our aquariums produce hard shells or skeletons. Corals build intricate structures beneath their tissues; clams, snails, shrimp, and many others produce hard parts; coralline algae, Halimeda spp. and some other algae reinforce their tissues too. Producing these structures is fundamental to the way in which these organisms live. The shells/skeletons provide the organisms that make them protection from predators and from harsh environmental conditions, and support their tissues, just as our bones support our bodies. All of these organisms calcify. That begs the question of what we mean when we say that they calcify; in other words, what is calcification? For a simple definition of calcification we might say it is:
Calcification: The process of precipitating calcium-rich minerals over an organic matrix.
If we use the analogy of constructing a building, the organic matrix, which is composed of specialized organic molecules made by the calcifying organisms, is rather like the scaffolding of the building. It is a small portion of the skeleton/shell and doesn’t provide any real strength, but instead provides the general pattern that allows the structure to begin taking shape. Calcium-rich minerals (various types of CaCO3 in these organisms) are like the concrete and the mortar that gives a building strength and provides the bulk of the structure.
An important point to consider is that these organisms are calcifying purposefully. Calcification is not simply a consequence of their activities, but rather a process they are putting energy and resources into. Calcium carbonate and other carbonates can and do precipitate abiotically both in our aquariums and in nature, without the aid of calcifying organisms, but at a fairly slow rate. It takes a great deal of energy and investment by these organisms to calcify at the high rates that are typical for them. Calcification is a process under strong biological control, though it is also strongly influenced by environmental conditions.
The rate that some organisms calcify may relate to how fast they can grow. For instance, corals that calcify faster are usually the ones that are able to grow faster, though the relationship between growth and calcification is not entirely straightforward. The rate of calcification and growth in corals can vary substantially for any given species, depending on environmental conditions. For example, rates of linear extension for the Caribbean Staghorn coral (Acropora cervicornis) have been measured in nature as low as 1 in yr-1 (Crabbe and Carlin, 2007) and as high as 10 in yr-1 (Lewis et al., 1968). If those growth rates were realized in an aquarium it would mean the difference between a golfball-sized coral colony growing into a baseball-sized colony in a year, or into a larger than basketball-sized colony in the course of that same year. That is a very big difference indeed. Most aquarists would probably prefer higher growth rates from their corals
and other organisms where possible. Faster growing organisms means that we have larger, more attractive animals in shorter periods of time, and more coral frags to trade and sell. It means a greater reward for our efforts and reduced impact on wild reefs by lessening the demand for wild-collected animals, both of which are very positive outcomes.
So how do we encourage our corals, clams, and other critters to grow quickly in our aquariums? What sorts of environmental conditions will favor growth rates near the upper end of the normal range, instead of nearer the lower end? Unfortunately there is no simple or single response sufficient to answer these questions, but there is a lot we can do to help our charges attain higher (and healthy) growth rates in captivity.
One of the most important considerations in encouraging rapid, healthy growth in corals and other calcifying organisms, and one that aquarists often struggle with, is in providing appropriate carbonate chemistry in our aquariums. Doing so involves manipulating several interacting variables, namely calcium concentration [Ca2+], magnesium concentration [Mg2+], total alkalinity, total CO2 and pH. These various parameters work together to form the carbonate system in sea water. Depending on how successful we are at manipulating these parameters we can arrive at conditions that allow for the rapid calcification and growth of our charges, or we can arrive at conditions that cause their calcified structures to dissolve away…literally. Providing appropriate carbonate chemistry in our aquaria is, more than almost any other consideration, absolutely critical to the continued good health and growth of our calcifying organisms.
While it is one of the most important aspects of keeping marine aquaria, few issues generate as many questions, or as much confusion, as how these parameters relate to each other, how best to go about manipulating them, and what sorts of targets to aim for with each of these parameters. In this series I will address all of these issues, and in ways that hopefully will make sense (or at least more sense) of this intriguing, complex system. But, as is always the case, it’s very hard to understand the significance of what we’re talking about if we don’t first understand what it is we’re talking about. This article will discuss each of the components of the carbonate system in sea water: what they are, what typical values are in natural sea water, and generally why they matter to aquarists.
The Major Components of Sea Water
To begin, let’s consider what is dissolved in sea water. Sea water is a complex chemical soup of dissolved minerals, dissolved gases, and a variety of dissolved and particulate organic materials. Salinity is a measure of the sum total of the dissolved minerals. To measure salinity, ideally we would like to be able to simply allow the water to evaporate away and measure the mass of the dissolved minerals. Unfortunately, when sea water is dried some of the components (namely carbonates and some halides) are lost to the atmosphere as gases. Several corrections have been used historically to take account of these losses, but the procedure to determine absolute salinity is very impractical for every-day use. Instead salinity is measured using the Practical Salinity Scale based on conductivity, or a related physical property such as refractive index or specific gravity. Because of the historical corrections needed in defining how salinity is measured there are actually slightly more than
35 g of dissolved minerals in 1 kg of sea water at a standard salinity of 35.000 (~35.171 g kg-1). Different dissolved components contribute distinct amounts to that total. For convenience, oceanographers typically split the components of sea water into three categories: major, minor, and trace components
Major components are those that contribute significantly to salinity. Since salinity is typically reported to 0.001 (1 ppm) by oceanographers, the components that typically have a concentration of 1 ppm or higher constitute the 11 major components of sea water. Minor components and trace elements are those that typically have a concentration lower than 1 ppm and therefore do not contribute measurably to salinity. The 11 major components and their typical concentrations in standard sea water are listed in Table 1. The contribution of these species to the total mass of dissolved solids can be seen in Figure 1. These 11 components include many of the components of interest for our discussion of carbonate chemistry.
| Component | g kg-1 | ppm | mmol kg-1 |
|---|---|---|---|
| Cations | |||
| Na+ | 10.7838 | 10,783.8 | 469.07 |
| Mg2+ | 1.2837 | 1283.7 | 52.82 |
| Ca2+ | 0.4121 | 412.1 | 10.28 |
| K+ | 0.3991 | 399.1 | 10.21 |
| Sr2+ | 0.0079 | 7.9 | 0.09 |
| Anions | |||
| Cl– | 19.3529 | 19,352.9 | 545.88 |
| SO42- | 2.7124 | 2,712.4 | 28.24 |
| HCO3– + CO32- | 0.1231 | 1231 | 2.02 |
| Br– | 0.0672 | 67.2 | 0.84 |
| B(OH)3 + B(OH)4– | 0.0272 | 27.2 | 0.41 |
| F– | 0.0013 | 1.3 | 0.07 |
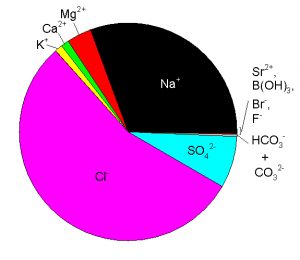
Figure 1. The relative mass contribution of the 11 major components of sea water to the total mass of dissolved solids. Values are for standard sea water.
The major components as well as some minor components of sea water show conservative behavior, meaning that the ratio of their concentration to salinity is constant in the ocean from place to place. Another way to say this is that the concentrations of these components are essentially the same in sea water everywhere around the world at a given salinity. A change in salinity therefore represents simply the gain or loss of water. Whether we measure the sea water in the Caribbean, off of Australia, Zanzibar, Finland, or Argentina, for any given salinity we’ll find the same concentration for all components that show conservative behavior. We can compare the concentration of a component from one place to another by normalizing the value to salinity as described by,
[MN] = [M]×(35/S)
The normalized concentration [MN] is equivalent to the concentration measured in our sample [M] times the ratio of standard salinity (35) to the salinity of our sample (S).
While the major components of sea water are generally conservative, this behavior can break down in some areas due to local processes. A few examples where conservative components may not be conservative are:
- Estuaries, where the outflow of rivers tends to disproportionately add Ca2+ and alkalinity, raising their ratios to salinity.
- The deep sea, where the dissolution of CaCO3 tends to elevate both Ca2+ and alkalinity relative to salinity. Due to the remineralization (= decomposition) of organic material, which tends to reduce the alkalinity slightly, the increase in alkalinity is smaller than that for Ca2+.
- Deep sea vents, which tend to reduce Mg2+, SO42-, and alkalinity relative to salinity.
Now let’s look more closely at the components of the carbonate system.
Calcium and Magnesium
Typically the units of measure used by aquarists to express Ca2+ and Mg2+ concentrations are ppm (parts per million). Normalized to a salinity of 35, the concentration of Ca2+ in sea water is about 412 ppm while that of Mg2+ is about 1284 ppm. That means that in 1 kg of sea water at a salinity of 35 we have 0.412 g Ca2+ and 1.284 g Mg2+. Of the parameters we will discuss, these two are probably the easiest for aquarists to visualize. When we measure the concentration of Ca2+ or Mg2+ we are simply measuring the mass of each ion dissolved in 1 kg of sea water.
While it is useful to discuss these parameters with regard to standard seawater (S = 35), salinity is not constant in the ocean. In areas where freshwater input (from rain and runoff) exceeds evaporation, the salinity of surface water drops. In areas where evaporation exceeds freshwater input, salinity rises. Salinity varies not only from region to region, based on local processes, but also seasonally in some places. While reefs may occur where the average salinity ranges from as low as 30 to as high as 42, most coral reefs occur where the average salinity is within the range 33-37. The concentrations of Ca2+ and Mg2+ will be about the same everywhere in the ocean when normalized to salinity, but variation in salinity from place to place means that there is some variation in Ca2+ and Mg2+ concentrations as well. For a salinity range of 33-37 we’d expect a range in Ca2+ concentration of about 388-436 ppm and a range in
Mg2+ concentration of about 1211-1357 ppm. Local processes can affect these values slightly as well. For example, coral reefs actively precipitate Ca2+ and to a smaller extent Mg2+ from the water column to form carbonate minerals, leading to slightly lower values for both. Dissolution of those minerals can also occur in parts of the reef (especially at night) yielding slightly higher values for Ca2+ and Mg2+ concentrations. Variation in Ca2+ and Mg2+ concentrations due to precipitation or dissolution of minerals on reefs is relatively small though (typically less than 10 ppm for Ca2+ and less than 3 ppm for Mg2+). Areas where upwelling occurs (e.g., Galapagos) may also experience slightly higher concentrations of Ca2+ as compared to areas that do not experience upwelling.
These two parameters are important for us to consider because both Ca2+ and Mg2+ (principally Ca2+) are building blocks used by calcifying organisms to build their skeletons. As we will see, Mg2+ plays an additional role in affecting the solubility of CaCO3 in sea water and rate of CaCO3 precipitation.
pH
Folks often have a bit more trouble understanding what pH actually measures as compared to a parameter such as Ca2+ concentration or Mg2+ concentration. This is an unfortunate artifact of the complicated-looking logarithmic scale used to express pH.
pH is how we show the quantity of hydrogen ions (H+, also referred to as “protons”) in water. Most quantities we measure are measured on linear scales. For example, a dumbbell that weighs 10 kg weighs twice as much as one of 5 kg and half as much as one of 20 kg. The logarithmic scale used to measure pH means that we see changes in [H+] that are orders of magnitude different: pH = 1 is ten times as acidic as pH = 2 and one million times as acidic as pH = 7.
pH is defined according to the following equation:
pH = -log(H+)
where (H+) is the activity of hydrogen ion. For water with very low ionic strength (very few dissolved ions), activity and concentration are essentially the same thing. We measure (H+) in molar units, that is, moles per liter of solution. Recall that 1 mole = Avogadro’s Number of particles (6.022 × 1023). If our solution has pH = 1 then we have an H+ concentration of 1 × 10-1 mol L-1. If the solution has pH = 7 we have an H+ concentration of 1 × 10-7 mol L-1. We could rewrite the equation above as
(H+) = 1 × 10-pH
Hence, a change of one pH unit means a change of one order of magnitude of (H+). A handy conversion to keep in minds is that a decrease of 0.3 pH units means we double (H+); an increase of 0.3 pH units means we cut (H+) in half. For example, at pH = 8.5, (H+) is half what it is at pH = 8.2. At pH = 7.9, (H+) is twice what it is at pH = 8.2. Even a relatively small change in pH means a big change in (H+), and potentially a big effect on any process influenced by pH.
While it is true that at very low ionic strength ion activity is essentially equivalent to ion concentration, as more and more ions are dissolved in water they begin to interact with each other in ways that makes the solution appear to have fewer ions than are actually present. That is, ion activity is lower than ion concentration in salty solutions. In sea water we have lots and lots of dissolved ions. H+ interacts strongly with SO42- to form HSO4– ion pairs, and with F– to form HF ion pairs. These ion pairs are short-lived, constantly forming and breaking apart, but nonetheless they affect the activity of H+. pH probes can only detect free H+ in water, not HSO4– or HF, so in effect that means that when we measure the pH of sea water we are only measuring a portion of the H+ present (~72.66% of the total concentration). This has important implications for
chemists and oceanographers and has led to the development of alternative pH scales for use in complex solutions, like sea water (the Total Scale, the Seawater Scale, and the Free Scale).
The pH scale used by aquarists and in most other applications is the one based off of buffers from the National Institute of Standards and Technology (NIST, formerly NBS, the National Bureau of Standards). Since the various pH scales are defined slightly differently, they give slightly different results. For example, standard sea water yields pHNIST = 8.20, pHT = 8.06, and pHSWS = 8.05 for the NIST, Total, and Seawater scales, respectively. Hence, the pH values quoted for sea water by oceanographers will be slightly lower than those measured by aquarists (by ~0.15 units). Hereafter, whenever I mention pH values they will be reported using the NIST scale used by aquarists. I mention the other pH scales so as to (hopefully) ease confusion for aquarists that may speak with oceanographers or read their writings. The pH of sea water measured by aquarists is ~0.15 units higher than the pH measured by oceanographers simply because we use different scales
of measure.
For our purposes the important thing to understand is that a pH measurement is telling us the quantity of H+ in the water and that the logarithmic scale used to measure pH means that a small change in pH represents a large change in (H+). Remember, an increase of 0.3 pH units means (H+) is cut in half; a 0.3 unit decrease means (H+) is doubled.
The pH in today’s shallow ocean averages 8.20, which is lower than the mean of 8.30 during the pre-industrial period. We’ll discuss why oceanic pH is lower today than it was in the recent past in later segments. In the open ocean, pH doesn’t vary much over the course of a day (perhaps 0.02 units), though it may show some seasonal variation related to variation in primary production. Around coral reefs we see a much higher density of organisms than in the open ocean. Their activities cause the pH in the water overlying reefs to vary much more than in nearby oceanic systems. Even on well-flushed outer reefs it’s not unusual to see a range of 0.2 pH units per day (e.g., pH ~8.1-8.3 over a 24 hr period). On reef flats, in lagoons, and areas with restricted water exchange it is possible to see much more variation in the course of a day. On some reef flats pH values have been measured to vary from as low as 7.8 to as high as 8.4 in a single 24 hr period (Yates and Halley, 2006). In some
lagoons, pH has been measured to vary as much as 1 pH unit in a day (e.g., 7.6 to 8.6). Seasonal and even multi-decadal cycles of pH variation in reef water have also been measured (Pelejero et al., 2005). While some of the pH values that organisms see in the field may be less than ideal for growth, many are able to tolerate a fairly wide range of pH values, at least for short periods of time.
One last point worth considering is that water (H2O) dissociates to produce two ions: hydrogen ion, H+, and hydroxide ion, OH–. The concentrations (technically the activities) of these two are inversely related. When there are a lot of H+ (low pH) there are few OH– and when there are few H+ (high pH) there are lots of OH–. Typically we think of pH = 7.00 as a neutral pH, meaning that (H+) = (OH–). While this is true at standard conditions (T = 25 °C, P = 1 atm) in a solution of low ionic strength, as temperature or pressure are changed, or in a solution of high ionic strength like sea water, the pH where (H+) = (OH–) changes slightly as well.
pH is an important parameter for us to consider for several reasons. Firstly, many physiological processes in living organisms are strongly affected by pH. If the pH of our tank water is substantially high or low, it may have direct, negative impacts on many of the organisms in our tanks, not just the calcifying organisms. In addition, pH plays a very important role in affecting the rate of CaCO3 precipitation and dissolution, as we will see.
Total CO2
The parameters we’ve discussed to this point are relatively straightforward. Calcium and magnesium concentration are merely the quantity of Ca2+ and Mg2+ dissolved in the water. While pH is measured using a somewhat cumbersome scale, it is merely the (apparent) quantity of H+ dissolved in the water. Discussing dissolved CO2 in water is necessarily more complex because instead of simply taking into account a single chemical species (Ca2+, Mg2+, or H+) here we must consider four different chemical species.
In the atmosphere, CO2 is a gas. That’s simple enough. When CO2 dissolves into water, however, some of it reacts chemically with that water to produce carbonic acid:
CO2(aq) + H2O ↔ H2CO3
In analytical chemistry, it is usually difficult to distinguish CO2(aq) from H2CO3, so the two are combined in a single term: CO2* ([CO2*] = [CO2(aq)] + [H2CO3]). Some of the carbonic acid will dissociate to produce a proton and a bicarbonate ion:
CO2* ↔ H+ + HCO3–
Some of the HCO3– will dissociate to produce a proton and a carbonate ion:
HCO3– ↔ H+ + CO32-
If we put all of that together we have a chemical equilibrium that looks like this:
CO2* ↔ H+ + HCO3– ↔ 2H+ + CO32-
It looks complicated, but let’s consider what it’s telling us. There are four different forms that CO2 takes in water (whether sea water or freshwater), though we’ve combined two of those terms for convenience. Since these chemical species interact with H+ we can see right away that the proportion of each will depend on the pH. If we have lots of H+ (= low pH) then the CO32- and HCO3– will take up some of the H+ and we will have mostly CO2*. If we have very few H+ (= high pH) then the CO2* and HCO3– will lose H+ and we will have mostly CO32-. At intermediate pH we’ll have mostly HCO3–, some CO2*, and some CO32-.
For many calculations in oceanography it is useful to know the total amount of CO2 in the water, regardless of which form it has taken. We call this parameter, aptly enough, total CO2, or TCO2. TCO2 is also written as CO2 and is equivalent in meaning to DIC (dissolved inorganic carbon). It is defined simply as the sum of the concentrations of each form of CO2,
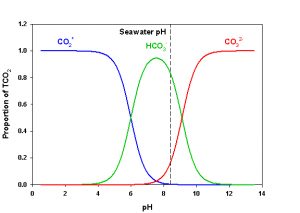
Figure 2. Speciation diagram for CO2 in sea water showing the relative proportion of each species. The speciation at normal seawater pH (pH = 8.20) is indicated by the dashed line. Values calculated for S =35, T = 25 °C, P = 1 atm.
TCO2 = [CO2*] + [HCO3–] + [CO32-]
Consulting Figure 2 we can see that in sea water at normal pH (= 8.20) we have mostly HCO3– (~88.4%), some CO32- (~11.0%) and only a small amount of CO2* (~0.54%). Of course, these proportions will change immediately if pH changes. If we add a strong acid (e.g., HCl) or a strong base (e.g., NaOH) to sea water, we will change the pH of that water, thereby changing the speciation of CO2. The pH therefore affects the speciation. However, we must also consider that if we add any of the CO2 species to sea water we will also affect the pH. For example, if we bubble CO2(g) into the water we will form carbonic acid, produce H+, and thereby lower pH. If we add CO32- some of the H+ in solution will be taken up to produce HCO3– and thereby raise pH. Temperature and pressure slightly affect the tendency of
CO2* to dissociate into H+ and HCO3– as well as the tendency of HCO3– to dissociate into H+ and CO32-. Said another way (for any chemists out there), temperature and pressure shift the dissociation constants pK1 and pK2 for carbonic acid. Varied salinity affects the activity of these species and thereby affects the apparent dissociation constants in sea water (pK1` and pK2`).
TCO2 can be measured directly, but doing so requires relatively sophisticated equipment. Instead of measuring TCO2, aquarists infer whether the TCO2 in their aquaria is high, low, or just right by measuring 1) tank pH, and 2) alkalinity, the next parameter of our discussion. For sake of completeness I will simply note that the TCO2 of standard sea water in equilibrium with today’s atmosphere is about 1991 µmol kg-1. TCO2 in sea water can vary over both short and long timescales, and variation in TCO2 has important consequences for our aquaria, and the ocean.
TCO2 is an important parameter for us to consider because the interaction between this parameter and total alkalinity largely controls the pH of sea water. TCO2 therefore plays a critical role in determining the rate of CaCO3 precipitation. TCO2 also affects the rate of photosynthesis in many organisms, which can further affect the rate of calcification in calcifying, photosynthetic organisms like corals and tridacnid clams.
Total Alkalinity
Oceanographers use the term total alkalinity whereas aquarists usually refer to the same property simply as alkalinity. We’ll see below why oceanographers include “total” to describe this aspect of seawater chemistry. I’ve saved alkalinity as the last parameter we’ll discuss because it is perhaps the most confusing for most aquarists. Indeed, even veteran aquarists often have a difficult time defining what alkalinity actually is. Total alkalinity can be defined in a few different ways, but I’ll use the definition that I believe will make the most sense to aquarists and that is most applicable to maintaining a marine aquarium.
But before we get to that definition, let’s recall that there are a lot of minerals dissolved in sea water. Some of the ions can accept protons and in so doing act as bases. Consider our discussion of TCO2 above. Bicarbonate ion can absorb up to one proton, to become carbonic acid,
HCO3– + H+ ↔ H2CO3
By the same token, carbonate ion can absorb up to two protons, to become carbonic acid,
CO32- + 2H+ ↔ H2CO3
While there are ions that can absorb protons, we already have some H+ in our water, and we have some ion pairs that will readily donate protons. Thus there are not only ions that act as proton acceptors (bases), there are also compounds that act as proton donors (acids):
HSO4– ↔ H+ + SO42-
HF ↔ H+ + F–
The total alkalinity is the capacity of the bases in sea water to neutralize additional H+, given that some H+ ions are already present. In other words, the total alkalinity is the capacity to buffer against a decrease in pH. More formally we’d say:
Total alkalinity: The excess concentration of proton acceptors (bases) over proton donors (acids) in a water sample when that sample is titrated to the carbonic acid endpoint (pH ~4).
Alkalinity is a property of sea water (or any solution) rather than the quantity of a single ion or compound. In this way it is much like salinity. The salinity of sea water is made up of many dissolved species, though just a few components constitute most of the total. Likewise, the majority of the total alkalinity in sea water is provided by just a few ions with all the rest contributing a tiny fraction. We can define total alkalinity with the equation,
TA = [HCO3–] + 2[CO32-] + [B(OH)4–] + [OH–] … – [H+] – [HSO4–] – [HF] – …
where “…” represents minor species.
Some of the total alkalinity is provided by bicarbonate and carbonate ions, collectively called carbonate alkalinity (CA = [HCO3–] + 2[CO32-]). Some is provided by borate [B(OH)4–], a bit is provided by hydroxide [OH–], and the small remainder is provided by a variety of other compounds (HPO42-, PO43-, Si(O2)–, MgOH+, etc.). When carbonate alkalinity, borate alkalinity, hydroxide alkalinity, and all other sorts of alkalinity are summed together, we have the total alkalinity. Measuring the alkalinity provided by just one of these components can often be challenging. In contrast, measuring the total alkalinity is comparatively easy and can be done precisely and accurately with fairly simple equipment.
In normal sea water (S = 35, pH = 8.20), HCO3– contributes by far the largest portion of the total alkalinity at 89.8%. Carbonate ion is the next largest contributor with 6.7% of the total. Summing those two together we can see that carbonate alkalinity alone constitutes 96.5% of the total alkalinity in normal sea water. Alkalinity in sea water is mostly provided by carbonate alkalinity. The other large contributor to total alkalinity is B(OH)4– at 2.9% of the total. Adding borate alkalinity and carbonate alkalinity together brings us to 99.4% of the total alkalinity contributed by just three species in normal sea water. Hydroxide contributes about 0.1% of the total alkalinity while all of the remaining sources of alkalinity combined contribute the remaining 0.5% in normal sea water.
In much the same way that temperature can be expressed on distinct scales yet measure precisely the same parameter (e.g., degrees Fahrenheit, degrees Celsius, Kelvins), aquarists commonly use three scales to express total alkalinity measurements:
- meq/L (millequivalents per liter)
- dKH (German degrees of carbonate hardness)
- ppm as CaCO3 (parts per million as CaCO3)
| Starting units | Convert to… | ||
|---|---|---|---|
| meq/L | dKH | ppm as CaCO3 | |
| meq/L | – | Multiply by 2.8 | Multiply by 50 |
| dKH | Divide by 2.8 | – | Multiply by 17.9 |
| ppm as CaCO3 | Divide by 50 | Divide by 17.9 | – |
Total alkalinity measurements can be readily converted from one scale to another (Table 2). Given that different scales are used to measure alkalinity, it is especially important to include units of measurement when discussing total alkalinity values with other aquarists. For example, an alkalinity measurement of “5” in a marine aquarium would be rather high if the unit of measure is meq/L, but quite low if the units are dKH. I will also simply note that oceanographers typically measure total alkalinity using a scale based on seawater mass instead of volume (meq kg-1 or µeq kg-1 vs. meq/L). Seawater mass is used by oceanographers because it can be measured more precisely than volume, and it is not subject to change with altered temperature or pressure whereas volume does change.
When normalized to S = 35, the total alkalinity of sea water averages about 2.35 meq/L (6.58 dKH) in the Atlantic and about 2.40 meq/L (6.72 dKH) in the Pacific. The small difference between oceans arises due to differences in the ages of the water masses in them (the “age” of a water mass being defined as the length of time since the water was in contact with the atmosphere). In the North Atlantic and in the Southern Ocean, near Antarctica, surface water sinks to the bottom of the ocean. This water then travels along the bottom of the Atlantic Ocean and past Antarctica. Along the journey CaCO3 particles produced by phytoplankton and other organisms in the shallow ocean sink and dissolve in the deep sea, slightly increasing the total alkalinity of the sea water. The deep water then upwells in the Pacific and Indian Oceans, yielding higher normalized total alkalinity there. After upwelling the water travels along the surface through the Pacific and Indian Oceans into the
Atlantic. Calcification by phytoplankton and other organisms removes a bit of the total alkalinity along the way and deposits it as CaCO3 particles in the deep ocean. Removal of alkalinity by calcifying organisms from the water as it makes its way to the Atlantic and the dissolution of those minerals as the water makes its way to the Pacific yields slightly lower normalized total alkalinity values in the Atlantic and slightly higher ones in the Pacific.
While the normalized total alkalinity does tend to be slightly higher in the Pacific than Atlantic, the higher salinity of the Atlantic Ocean yields slightly higher absolute total alkalinity values there. Just as with Ca2+ and Mg2+ above, variation in salinity from place to place causes some variation in absolute total alkalinity values as well. Total alkalinity ranges over ~2.35-2.48 meq/L (6.58-6.94 dKH) in the Atlantic (S ~35-37) vs. 2.27- 2.42 meq/L (6.36-6.78 dKH) in the Pacific (S ~33-35).
All of these values fall within the error of measurement of most hobbyist test kits though. While total alkalinity values of 2.3-2.5 meq/L (6.4-7.0 dKH) are readily distinguishable to an oceanographer with good equipment, hobbyist test kits are not precise enough to measure such small differences reliably.
Total alkalinity is an important parameter for us to consider for several reasons. First, it helps to stabilize our pH and buffer against a drop in pH. Second, the interaction between total alkalinity and total CO2 largely controls seawater pH, as we will see. Third, HCO3– and CO32-, for which total alkalinity is a proxy, constitute building blocks for CaCO3 shells and skeletons. Hence, the alkalinity of sea water is intimately connected to the carbonate system in several ways.
| Component | Mean value |
|---|---|
| Ca2+ | 412 ppm |
| Mg2+ | 1284 ppm |
| pH | 8.20 |
| Total CO2 | 1991 µmol kg-1 |
| Total alkalinity | 2.35 meq/L = 6.58 dKH = 119 ppm as CaCO3 |
Conclusion
In this article we’ve identified the major components of the carbonate system in sea water. Mean values for each of these parameters are summarized in Table 3. All of these components can be directly manipulated by the aquarist. By understanding the carbonate system and using that knowledge to our advantage it is possible to encourage rapid calcification and growth in many of the calcifying organisms we maintain in captivity. Next month we’ll discuss how these components work together to provide the chemistry we measure in the aquarium, and in the ocean.
References
- Crabbe JMC, Carlin JP (2007) Industrial sedimentation lowers coral growth rates in a turbid lagoon environment, Discovery Bay, Jamaica. IJIB 1:37-40.
- Lewis JB, Axelsen F, Goodbody I, Page C, Chislett G (1968) Comparative growth rates of some reef corals in the Caribbean. McGill Univ Mar Sci Cent Manuscr 10:1-26.
- Millero FJ (2006) Chemical Oceanography, Third Edition. Taylor and Francis Group, Boca Raton, FL.
- Pelejero C, Calvo E, McCulloch MT, Marshall JF, Gagan MK, Lough JM, Opdyke BN (2005) Preindustiral to modern interdecadal variability in coral reef pH. Science 309:2204-2207.
- Yates KK, Halley RB (2006) CO32- concentration and pCO2 thresholds for calcification and dissolution on the Molokai reef flat, Hawaii. Biogeosci 3:357-369.


0 Comments