Every aquarist at one time or another has had to deal with plumbing issues such as sizing of pumps, selecting pipe size, determining whether the pump can be upgraded without changing the returns in the overflow box, maintaining water flow while controlling velocity so that it does not blow off the coral tissue, etc.
A lot of this information is available in the form of “rules of thumb” as well as established fluids engineering formulas and data. This is an attempt to explain the basics of the devices used to create and manage water flow and to provide a better understanding of the principles involved as well as trying to consolidate the relevant information for an aquarist in one single document.
In addition to providing the theory, formulas and tables of relevant data, for practical use we also provide an Excel spreadsheet that incorporates all the useful information in a useable form, without the requirement that the user understand the math and formulas needed for solving the plumbing design problems.
Pump Basics
Pumps are the most common devices used to move water through the filters, skimmers, and create circulation in the tanks. The most common type of pump used is called the centrifugal pump. The centrifugal pump is basically a rotary machine and comprises 3 main elements.
- The impeller – rotating element
- The volute- the casing inside which the impeller rotates
- The motor – imparts the rotation to the impeller
The pump functions by converting the rotational energy of the motor to kinetic energy of the liquid by accelerating the liquid from the center of the impeller to the outer via centrifugal force. The amount of energy imparted depends on the velocity of the liquid at the tip of the impeller. Similar to rotating an object tied to a string, the velocity will be higher if the speed of rotation is higher or the diameter of the impeller is larger. The volute of the pump harnesses this kinetic energy by creating a resistance to the flow and slowing it down, this results in the creation of pressure energy. So in reality a centrifugal pump only creates flow, and the resistance to this flow is what creates the pressure. Flow is typically measured in GPH (Gallons per Hour) or GPM (Gallons per Minute).
The impeller is driven by a motor and is usually connected to the motor in 2 ways. Direct coupling to the motor via a shaft – called direct drive pumps, magnetically coupled.
Pumps with the impellers directly connected to the motor via the shaft require the use of a mechanical seal, which are prone to failure and end up with leaks. The magnetic coupled pumps avoid the seal problem by using magnets to drive the impeller, thus allowing the creation of a centrifugal pump that does not require a mechanical seal. For reef aquarium applications the best choice is typically the magnetically driven centrifugal pump and most of the common brands are of this design.
The kinetic energy that is created by the pump is often measured as head. Head refers to the height of a liquid column which the pump could create using the kinetic energy that is generated by the pump. If the discharge of the pump is pointed straight up into the air, it will pump the fluid to a certain height – the maximum head or shut off head. This is usually determined by the speed of the motor and outside diameter of the pumps impeller.
The amount of fluid the pump moves is measured by the flow rate in GPH or GPM. The flow rate can be converted to velocity of fluid as follows:
- Velocity = feet/sec
- GPM = Gallons per Min
- D = Inside diameter of pipe in inches
From this we can see the first important observation about velocity and pipe diameter. Doubling the pipe diameter will decrease the velocity by a factor of 4.
Pumps are rated by flow rate, head, and power consumption. When designing an aquarium system we are concerned with X amount of flow at Y amount of head. Each pump will have its own relationship between head and flow rate, depending on the pump design, and this information will typically be displayed on the pump performance curve. For any pump, the flow rate will reduce as the amount of head increases.
Pipes and Piping Systems
The flow of the pump is channeled through pipes and the piping system comprising the pipes, fittings, control valves, etc. Solving fluid flow problems requires the use of a few basic equations. The first one is the simple law of conservation of mass, where the flow rate between any 2 sections is conserved.
The second is the energy equation between any 2 sections of a pressurized pipe. The energy equation between any two sections of a pressurized pipe can be written as
Where:
- Z = elevation of centerline of pipe relative to an arbitrary datum
- P = pressure on centerline of pipe
- γ = Specific Weight of Fluid
- V = average flow velocity
- Hf = head loss due to friction
- Hm = minor losses
As the water flows through the pipe and piping system it encounters resistance, primarily due to the following 3 elements: resistance due to the elevation it has to raise the water – called static head, or static head loss resistance due to friction with the walls of the pipe – friction loss resistance due to the fittings and valves used in the piping system.
The cumulative effect of this resistance is to reduce the resulting flow at the outlet. This cumulative resistance is often measured in terms of head or pressure loss, and also called the total dynamic head (TDH) of the piping systems.
To determine the flow parameters at the outlet we need to compute the TDH. Let us look at each one of the components separately:
Resistance due to elevation – Static Head
The pump is used to move the liquid from a lower point to a higher point. The difference between the height of the liquid levels at the output and input of the pump is the static head.
Friction Loss in Pipes
As the fluid flows through the pipe, friction on the side walls of the pipe create resistance to the flow. Two approaches are used to estimate the friction loss:
- Using published tables
- Using the governing equations
1) Using Published Tables
Tables indicating friction loss are available at several web sites, one such table is published below as Table 1. These tables are typically derived using the empirical formula called the Hazen-Williams formula. This formula is as follows:
Where:
- Hf = Friction loss in feet of head
- L = Length of pipe in feet
- Q = flow rate in GPM
- D = Nominal pipe ID in inches
- C = friction factor from Hazen-Williams
The value of C is critical for computation and relates to the roughness of the interior wall of the pipe. One of the reasons that you find that tables are not identical is due to the fact that different values of C are used for the same material. For PVC pipe the value of C ranges from 140 to 150.
The Hazen Williams formula has a limited range of validity and is only valid for turbulent flow with reasonable velocity [Ref. C.P. Liou]. However, for the range of typical values in a reef aquarium the formula is quite valid.
| GPM | 1/2″ | 3/4″ | 1″ | 1 1/4″ | 1 1/2″ | 2″ | 3″ | 4″ |
|---|---|---|---|---|---|---|---|---|
| 1 | 2.08 | 0.51 | – | – | – | – | – | – |
| 2 | 4.16 | 1.02 | 0.55 | 0.14 | 0.07 | – | – | – |
| 5 | 23.44 | 5.73 | 1.72 | 0.44 | 0.22 | 0.066 | 0.015 | – |
| 7 | 43.06 | 10.52 | 3.17 | 0.81 | 0.38 | 0.11 | 0.021 | – |
| 10 | 82.02 | 20.04 | 6.02 | 1.55 | 0.72 | 0.21 | 0.03 | – |
| 15 | – | 42.46 | 12.77 | 3.28 | 1.53 | 0.45 | 0.07 | – |
| 20 | – | 72.34 | 21.75 | 5.59 | 2.61 | 0.76 | 0.11 | 0.03 |
| 25 | – | – | 32.88 | 8.45 | 3.95 | 1.15 | 0.17 | 0.04 |
| 30 | – | – | 46.08 | 11.85 | 5.53 | 1.62 | 0.23 | 0.06 |
| 35 | – | – | – | 15.76 | 7.36 | 2.15 | 0.31 | 0.08 |
| 40 | – | – | – | 20.18 | 9.43 | 2.75 | 0.41 | 0.11 |
| 45 | – | – | – | 25.1 | 11.73 | 3.43 | 0.51 | 0.17 |
| 50 | – | – | – | 30.51 | 14.25 | 4.16 | 0.61 | 0.16 |
| 60 | – | – | – | – | 19.98 | 5.84 | 0.85 | 0.22 |
| 70 | – | – | – | – | – | 7.76 | 1.13 | 0.31 |
| 75 | – | – | – | – | – | 8.82 | 1.28 | 0.34 |
| 80 | – | – | – | – | – | 9.94 | 1.44 | 0.38 |
| 90 | – | – | – | – | – | 12.37 | 1.8 | 0.47 |
| 100 | – | – | – | – | – | 15.03 | 2.18 | 0.58 |
2) Using the Governing Equations
This approach is based on using the Darcy-Wiesenbach equation and is valid for all types of flow. This approach is the one most commonly used in software packages for fluid flow analysis. The Darcy-Weisbach method is generally considered more accurate than the Hazen-Williams method. Additionally, the Darcy-Weisbach method is valid for any liquid or gas; Hazen-Williams is only valid for water at ordinary temperatures (40 to 75o F). The Hazen-Williams method is very popular, especially among civil engineers, since its friction coefficient (C) is not a function of velocity or pipe diameter. Hazen- Williams is simpler than Darcy-Weisbach for calculations where you are solving for flowrate, velocity, or diameter.
The main governing equation for friction loss is Darcy’s equation
Where:
- Hf = friction loss in feet of head
- f = dimensionless friction factor
- L = Pipe Length in FEET
- D = Pipe Inside Diameter in FEET
- V = Flow Velocity in FEET PER SECOND
- g = Gravitational Constant = 32.2 feet per second squared
From this equation it is quite clear that the flow velocity has a big impact on frictional losses. From equation 1 we know that the flow velocity is inversely proportional to the square of the pipe diameter. So if we reduce the pipe diameter by ½, we increase the flow velocity by a factor of 4 and hence also increase the friction loss by a factor of 16.
To apply this equation we need to determine the friction factor f, which is the complicated part. The steps are as follows:
We first need to determine the type of flow which is typically determined from the Reynold’s number, which rates the type of flow in the pipe: Laminar, Turbulent or Transitional flow. The Reynold’s number is a dimensionless number and is calculated as follows
- D = diameter of pipe in Feet
- V = velocity in Feet/sec
- μ = kinematic viscosity of the fluid being pumped
The kinematic viscosity is the ratio of the fluid’s density and the fluids absolute viscosity. The kinematic viscosity changes according to temperature, see table (www.pump.net)
| Temp (degrees F) | Kinematic Viscosity of fresh water |
|---|---|
| 70 | 1.0265 x 10-5 ft2/sec |
| 75 | 9.6199 x 10-6 ft2/sec |
| 80 | 9.0363 x 10-6 ft2/sec |
Kinematic Viscosity is the ratio of the fluid’s density and the fluid’s absolute viscosity. These values are for FRESH water. For saltwater multiply the kinematic viscosity of water by 1.024 (or whatever your planned specific gravity will be).
This Reynolds Number will tell us whether a particular flow is laminar, in the transition zone, or is turbulent, and the following chart gives the generally accepted ranges for these flows:
| Reynolds Number | Flow Type |
|---|---|
| RD < 2300 | Laminar |
| 2300 < RD < 4000 | Transitional |
| 4000 < RD | Turbulent |
For most of our application the flow through the pipes will generally be turbulent.
Once the type of flow is determined, the next step is to calculate the friction factor.
The Moody Equation is used to calculate the dimensionless friction factor f. and originates from a paper published by Lewis F. Moody in 1944. Typically the values can be read off a Moody diagram (see http://www.mestudent.com/fluids/moody.htm for a Moody Chart) which is created using the Colebrook-White formula
Where:
- f is the friction factor
- ε = roughness factor (generally .000005 ft for PVC pipe.)
- D = diameter in inches
- Re = Reynold’s number
The equation is difficult to solve in close form since f appears on both sides of the equation. It has to be solved numerically.
The Swamee-Jain approximation can be used to calculate the friction factor under certain conditions (where ε/D < .02 and Re > 3000), and gives results within 3% of the results obtained from the Moody diagram. It has the advantage of being easily programmed in a computer or calculator. For most of the aquarium applications the flow is turbulent. The Swamee-Jain approximation for the friction factor is as follows:
Another alternate formula given by Haaland as follows can be used and the result varies less than 2% of the Moody Chart. [Reference].
Using this, as an example let us compute the friction loss in 100ft of 1” PVC pipe with a flow rate of 30 GPM for saltwater at 80oF.
Given:
- L =100ft
- D = 1.049” (A 1” pipe has dimension of 1.049”)
- Q = 20 GPM
- μ = 9.0363 x 10-6 ft2/sec * 1.024 = 9.2521 x 10-6 ft2/sec
- Velocity = 0.4085*30/(1.049)2 = 11.136 ft/sec
The friction factor f computed using Swamme-Jain equation = 0.01926
The total friction loss Hf = 39.71
The value according to the published charts (based on Hazen-Williams) for PVC schedule 40 pipe is 46.08 and is more conservative than the result obtained using the governing equations.
Minor Losses
For any pipe system, in addition to the friction losses, there are additional losses called minor losses (although in our case these losses may far exceed the friction loss). These losses arise due to the pipe entrance and exit, sudden expansion or contraction, bends, elbows, and other fittings, valves, etc.
Here again the empirical method can be used to determine the resistance due to the fittings. The friction loss in the table 4 below is expressed in terms of equivalent feet of straight pipe. What this means is that the amount of friction created by the fittings is the same as that of the specified straight pipe. We can add this length of straight pipe to the total pipe length in the system and compute the friction loss.
| Fitting | 1/2″ | 3/4″ | 1″ | 1 1/4″ | 1 1/2″ | 2″ | 3″ | 4″ |
|---|---|---|---|---|---|---|---|---|
| 90 ELBOW | 1.5 | 2 | 2.25 | 4 | 4 | 6 | 8 | 12 |
| 45 ELBOW | 0.75 | 1 | 1.4 | 1.75 | 2 | 2.5 | 4 | 5 |
| GATE VALVE | 0.3 | 0.4 | 0.6 | 0.8 | 1 | 1.5 | 2 | – |
| TEE-Flow-RUN | 1 | 1.4 | 1.7 | 2.3 | 2.7 | 4.3 | 6.3 | 8.3 |
| TEE-Flow-Branch | 4 | 5 | 6 | 7 | 8 | 12 | 16 | 22 |
Another more acceptable approach is to use the loss coefficient of each entity in the plumbing system (often measured experimentally and correlated to pipe flow parameters).
The head loss across each fitting is then obtained using this equation:
Where:
- Hm = head loss in feet
- K = loss coefficient
- V = velocity in Ft per Second
- g = gravity 32.2 ft/s2
The resistance coefficients (K) for the valves and fittings are available as tables. A good source is for these coefficients is www.pump.net. Table 5 reproduced below can be found at http://pump.net/frictiondata/friclossfittings.htm . In addition to providing the K values, this table also has a column for L/D. This L/D can also be used directly in equation (5) to calculate the friction loss for each fitting. One piece of data missing from table 5 is the K or L/D values for coupling or union fittings which are a common item in aquarium plumbing. Typically quoted values of K for coupling/union range between 0.02-0.04, with L/D=2.
| Fitting | L/D | Nominal Pipe Size | |||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ½ | ¾ | 1 | 1¼ | 1½ | 2 | 2½-3 | 4 | 6 | 8-10 | 12-16 | 18-24 | ||||||||||||||||||
| K Value | |||||||||||||||||||||||||||||
| Angle Valve | 55 | 1.48 | 1.38 | 1.27 | 1.21 | 1.16 | 1.05 | 0.99 | 0.94 | 0.83 | 0.77 | 0.72 | 0.66 | ||||||||||||||||
| Angle Valve | 150 | 4.05 | 3.75 | 3.45 | 3.30 | 3.15 | 2.85 | 2.70 | 2.55 | 2.25 | 2.10 | 1.95 | 1.80 | ||||||||||||||||
| Ball Valve | 3 | 0.08 | 0.08 | 0.07 | 0.07 | 0.06 | 0.06 | 0.05 | 0.05 | 0.05 | 0.04 | 0.04 | 0.04 | ||||||||||||||||
| Butterfly Valve | – | – | – | – | – | – | 0.86 | 0.81 | 0.77 | 0.68 | 0.63 | 0.35 | 0.30 | ||||||||||||||||
| Gate Valve | 8 | 0.22 | 0.20 | 0.18 | 0.18 | 0.15 | 0.15 | 0.14 | 0.14 | 0.12 | 0.11 | 0.10 | 0.10 | ||||||||||||||||
| Globe Valve | 340 | 9.2 | 8.5 | 7.8 | 7.5 | 7.1 | 6.5 | 6.1 | 5.8 | 5.1 | 4.8 | 4.4 | 4.1 | ||||||||||||||||
| Plug Valve Branch Flow | 90 | 2.43 | 2.25 | 2.07 | 1.98 | 1.89 | 1.71 | 1.62 | 1.53 | 1.35 | 1.26 | 1.17 | 1.08 | ||||||||||||||||
| Plug Valve Straightaway | 18 | 0.48 | 0.45 | 0.41 | 0.40 | 0.38 | 0.34 | 0.32 | 0.31 | 0.27 | 0.25 | 0.23 | 0.22 | ||||||||||||||||
| Plug Valve 3-Way Thru-Flow | 30 | 0.81 | 0.75 | 0.69 | 0.66 | 0.63 | 0.57 | 0.54 | 0.51 | 0.45 | 0.42 | 0.39 | 0.36 | ||||||||||||||||
| Standard Elbow | 90° | 30 | 0.81 | 0.75 | 0.69 | 0.66 | 0.63 | 0.57 | 0.54 | 0.51 | 0.45 | 0.42 | 0.39 | 0.36 | |||||||||||||||
| 45° | 16 | 0.43 | 0.40 | 0.37 | 0.35 | 0.34 | 0.30 | 0.29 | 0.27 | 0.24 | 0.22 | 0.21 | 0.19 | ||||||||||||||||
| long radius 90° | 16 | 0.43 | 0.40 | 0.37 | 0.35 | 0.34 | 0.30 | 0.29 | 0.27 | 0.24 | 0.22 | 0.21 | 0.19 | ||||||||||||||||
| Close Return Bend | 50 | 1.35 | 1.25 | 1.15 | 1.10 | 1.05 | 0.95 | 0.90 | 0.85 | 0.75 | 0.70 | 0.65 | 0.60 | ||||||||||||||||
| Standard Tee | Thru-Flow | 20 | 0.54 | 0.50 | 0.46 | 0.44 | 0.42 | 0.38 | 0.36 | 0.34 | 0.30 | 0.28 | 0.26 | 0.24 | |||||||||||||||
| Thru-Branch | 60 | 1.62 | 1.50 | 1.38 | 1.32 | 1.26 | 1.14 | 1.08 | 1.02 | 0.90 | 0.84 | 0.78 | 0.72 | ||||||||||||||||
| 90 Bends, Pipe Bends, Flanged Elbows, Butt-Welded Elbows | r/d=1 | 20 | 0.54 | 0.50 | 0.46 | 0.44 | 0.42 | 0.38 | 0.36 | 0.34 | 0.30 | 0.28 | 0.26 | 0.24 | |||||||||||||||
| r/d=2 | 12 | 0.32 | 0.30 | 0.28 | 0.26 | 0.25 | 0.23 | 0.22 | 0.20 | 0.18 | 0.17 | 0.16 | 0.14 | ||||||||||||||||
| r/d=3 | 12 | 0.32 | 0.30 | 0.28 | 0.26 | 0.25 | 0.23 | 0.22 | 0.20 | 0.18 | 0.17 | 0.16 | 0.14 | ||||||||||||||||
| r/d=4 | 14 | 0.38 | 0.35 | 0.32 | 0.31 | 0.29 | 0.27 | 0.25 | 0.24 | 0.21 | 0.20 | 0.18 | 0.17 | ||||||||||||||||
| r/d=6 | 17 | 0.46 | 0.43 | 0.39 | 0.37 | 0.36 | 0.32 | 0.31 | 0.29 | 0.26 | 0.24 | 0.22 | 0.20 | ||||||||||||||||
| r/d=8 | 24 | 0.65 | 0.60 | 0.55 | 0.53 | 0.50 | 0.46 | 0.43 | 0.41 | 0.36 | 0.34 | 0.31 | 0.29 | ||||||||||||||||
| r/d=10 | 30 | 0.81 | 0.75 | 0.69 | 0.66 | 0.63 | 0.57 | 0.54 | 0.51 | 0.45 | 0.42 | 0.39 | 0.36 | ||||||||||||||||
| r/d=12 | 34 | 0.92 | 0.85 | 0.78 | 0.75 | 0.71 | 0.65 | 0.61 | 0.58 | 0.51 | 0.48 | 0.44 | 0.41 | ||||||||||||||||
| r/d=14 | 38 | 1.03 | 0.95 | 0.87 | 0.84 | 0.80 | 0.72 | 0.68 | 0.65 | 0.57 | 0.53 | 0.49 | 0.46 | ||||||||||||||||
| r/d=16 | 42 | 1.13 | 1.05 | 0.97 | 0.92 | 0.88 | 0.80 | 0.76 | 0.71 | 0.63 | 0.59 | 0.55 | 0.50 | ||||||||||||||||
| r/d=18 | 45 | 1.24 | 1.15 | 1.06 | 1.01 | 0.97 | 0.87 | 0.83 | 0.78 | 0.69 | 0.64 | 0.60 | 0.55 | ||||||||||||||||
| r/d=20 | 50 | 1.35 | 1.25 | 1.15 | 1.10 | 1.05 | 0.95 | 0.90 | 0.85 | 0.75 | 0.70 | 0.65 | 0.60 | ||||||||||||||||
| Mitre Bends | a=0° | 2 | 0.05 | 0.05 | 0.05 | 0.04 | 0.04 | 0.04 | 0.04 | 0.03 | 0.03 | 0.03 | 0.03 | 0.02 | |||||||||||||||
| a=15° | 4 | 0.11 | 0.10 | 0.09 | 0.09 | 0.08 | 0.08 | 0.07 | 0.07 | 0.06 | 0.06 | 0.05 | 0.05 | ||||||||||||||||
| a=30° | 8 | 0.22 | 0.20 | 0.18 | 0.18 | 0.17 | 0.15 | 0.14 | 0.14 | 0.12 | 0.11 | 0.10 | 0.10 | ||||||||||||||||
| a=45° | 15 | 0.41 | 0.38 | 0.35 | 0.33 | 0.32 | 0.29 | 0.27 | 0.26 | 0.23 | 0.21 | 0.20 | 0.18 | ||||||||||||||||
| a=60° | 25 | 0.68 | 0.63 | 0.58 | 0.55 | 0.53 | 0.48 | 0.45 | 0.43 | 0.38 | 0.35 | 0.33 | 0.30 | ||||||||||||||||
| a=75° | 40 | 1.09 | 1.00 | 0.92 | 0.88 | 0.84 | 0.76 | 0.72 | 0.68 | 0.60 | 0.56 | 0.52 | 0.48 | ||||||||||||||||
| a=90° | 60 | 1.62 | 1.50 | 1.38 | 1.32 | 1.26 | 1.14 | 1.08 | 1.02 | 0.90 | 0.84 | 0.78 | 0.72 | ||||||||||||||||
| Note: Fittings are standard with full openings. | |||||||||||||||||||||||||||||
| Fitting | L/D | Minimum Velocity for Full Disc Lift | Nominal Pipe Size | |||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ½ | ¾ | 1 | 1¼ | 1½ | 2 | 2½-3 | 4 | 6 | 8-10 | 12-16 | 18-24 | |||||||||||||||||||
| General ft/sec | Water ft/sec | K Value | ||||||||||||||||||||||||||||
| Swing Check Valve | 100 | 35 v1/2 | 4.40 | 2.70 | 2.50 | 2.30 | 2.20 | 2.10 | 1.90 | 1.80 | 1.70 | 1.50 | 1.40 | 1.30 | 1.20 | |||||||||||||||
| 50 | 48 v1/2 | 6.06 | 1.40 | 1.30 | 1.20 | 1.10 | 1.10 | 1.00 | 0.90 | 0.90 | 0.75 | 0.70 | 0.65 | 0.60 | ||||||||||||||||
| Lift Check Valve | 600 | 40 v1/2 | 5.06 | 16.2 | 15.0 | 13.08 | 13.2 | 12.6 | 11.4 | 10.8 | 10.2 | 9.0 | 8.4 | 7.8 | 7.2 | |||||||||||||||
| 55 | 140 v1/2 | 17.7 | 1.50 | 1.40 | 1.30 | 1.20 | 1.20 | 1.10 | 1.00 | 0.94 | 0.83 | 0.77 | 0.72 | 0.66 | ||||||||||||||||
| Tilting Disc Check Valve | 5 | 80 v1/2 | 10.13 | – | – | – | – | – | 0.76 | 0.72 | 0.68 | 0.60 | 0.56 | 0.39 | 0.24 | |||||||||||||||
| 15 | 30 v1/2 | 3.80 | – | – | – | – | – | 2.30 | 2.20 | 2.00 | 1.80 | 1.70 | 1.20 | 0.72 | ||||||||||||||||
| Foot Valve with Strainer Poppet Disc | 420 | 15 v1/2 | 1.90 | 11.3 | 10.5 | 9.70 | 9.30 | 8.80 | 8.00 | 7.60 | 7.10 | 6.30 | 5.90 | 5.50 | 5.0 | |||||||||||||||
| Foot Valve with Strainer Hinged Disc | 75 | 35 v1/2 | 4.43 | 2.00 | 1.90 | 1.70 | 1.70 | 1.70 | 1.40 | 1.40 | 1.30 | 1.10 | 1.10 | 1.00 | 0.90 | |||||||||||||||
| Fitting | Description | All Pipe Sizes |
|---|---|---|
| K Value | ||
| Pipe Exit | Projecting Sharp-Edged Rounded | 1.00 |
| Pipe Entrance | Inward Projecting | 0.78 |
| Pipe Entrance Flush | Sharp-Edged | 0.50 |
| r/d=0.02 | 0.28 | |
| r/d=0.04 | 0.24 | |
| r/d=0.06 | 0.15 | |
| r/d=0.10 | 0.09 | |
| r/d<0.14 | 0.04 |
The power required to pump the fluid is given by:
and 1 HP = 746 Watts
System Performance Curve & Operating Point
The system performance curve is the mapping of head required to produce flow in a given system. A system includes all the pipes, fitting and devices the fluid must flow through and represents the frictional and static loss the fluid experiences.
The operating point of the plumbing system is the point at which the pump performance curve intersects the system curve (see Figure 1). This typically requires an iterative solution to determine the point of intersection, and becomes tedious by hand. Selecting a pump requires that these calculations be repeated for different pumps to determine the operating point for the different pumps. Also if different plumbing systems are to be evaluated this would require that the different systems performance curves are generated.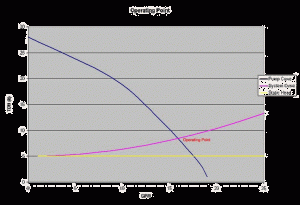
A use of spreadsheet or computer software is required. There are several commercially available software packages that will do this, however these are not free. A sample spread sheet is included along with this article. It is my hope that this will eventually evolve over time to become a complete plumbing system design tool for reef hobbyists.
Example Design Scenario
To help in understanding the concepts presented, consider a simple circulation loop to be designed for an aquarium system shown in figure 2 below: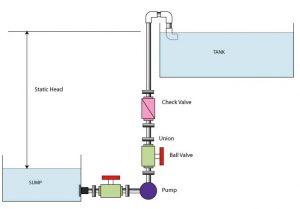
The design problem can take one of several forms:
- Given the pump and size of piping system, fittings, valves, and plumbing schematic, what will be the resulting flow and velocity at the output?
- Given a desired flow rate and velocity at output, what size pump and piping schematic should be used?
- Given the piping system, what is the best pump to use for the job?
Scenario #1
Let us assume for starters that the system designer has determined that the pump to be used is an Iwaki 55 RLT with a 1” outlet and inlet, and the piping system used a PVC Schedule 40 pipe of nominal diameter 1.” We need to know what the flow rate and velocity will be at the output in the tank. Given the inter relationships between friction and flow the problem needs to be solved in an interactive manner. We start with a guess as the initial solution. A good initial guess may be made by just using the static head of the system and the pump performance curve. Let’s start with a guess of say 780GPH or 13 GPM.
Step 1: Compute the friction head
Calculate the Reynold’s number using formula, and the kinetic viscosity of saltwater at 80o F
- Re = 45600
Compute the friction factor f, either by using the Moody Chart or Swamee-Jain approximation, using ε = 0.000005 ft for PVC pipe
- f = 0.0214
Using Darcy-Wiesenbach equation compute the friction head
- Hf = .5316 ft
Step 2: Compute the Minor Losses
Follow the path of the water flow all the way from the input to the output, and tabulate all the entities that would contribute to the minor losses, along with their K value.
| Fitting | Number | K |
|---|---|---|
| Pipe Size | 1” | |
| # of ball valves | 2 | 0.14 |
| Gate Valve | 0 | 0 |
| # of Elbows – 90 | 3 | 2.07 |
| # of Elbows-45 | 0 | 0 |
| # of Couplings/Union | 6 | 0.18 |
| #of Swing Check Valve | 1 | 1.2 |
| Sudden Expansion | 0 | 0 |
| pipe Exit | 1 | 1 |
| Pipe Entrance | 0.5 | 0.5 |
| Total K | 5.09 | |
| Minor Head Loss | 1.776 |
Using the basic energy equation:
- The total dynamic head (TDH) = Static Head + Friction Head + Minor Head loss
- TDH = 5 ft + .7615 ft + 1.776 = 7.03 ft
From the pump chart we can see that the flow rate at TDH of 7.03 ft is 16GPM or 960GPH, which is higher than the initial guess. So we would have to increase the guess and resolve. Solving this iteratively gives a flow rate of 15.9 GPM (954 GPH) at a TDH of 8.412 ft with an output velocity of 5.9 ft/sec. The change in TDH in this case did not affect the flow much since this is a pressure rated pump.
Scenario #2
Now let us consider the same problem but using 1.5” Schedule 40 PVC pipe. An additional fitting, a male adaptor 1” to 1.5” will need to be added. In this case the flow will be 1025 GPH at a TDH of 5.66 ft. By upsizing the pipe from 1” to 1.5” the TDH was reduced by 2.752’ or nearly 1/3rd. This is really amazing considering that 5’ of the TDH is pure static head height so the friction and minor losses using the 1.5” pipe is only .66’! This would make a much more significant difference on a pump with a flatter performance curve. Clearly upsizing the pipe to one size higher will result in more flow at lower velocity – at 2.69 ft/sec. By increasing the size of pipe that is used you get a higher flow rate with a lower velocity using the same pump.
This is using an Iwaki 55 pump which does fairly well in most pressure rated applications. Let’s say you want to use a pure circulation pump like the Ampmaster 3000 but would still like to use 1” plumbing. Solving for the final flow rate using the governing equations you would end up with a flow rate of 1,516 gph at a TDH of 11.89 ft with an output velocity of 9.37 ft/sec. Increasing the size of the plumbing to 1.5” for the ampmaster would increase the flow rate to 2,475 gph at a TDH of 7.93 ft with an output velocity of 6.49 ft/sec. Nearly 1,000 gph additional flow rate and because of the larger sized plumbing the velocity has actually been reduced.
Practical Issues and use of this Spreadsheet
The proper plumbing setup can be as important if not even more important than the pump or pumps that you end up choosing. The calculations provided are intended to be a tool to help you determine the best plumbing and pump setup for you.
The biggest key to designing the best plumbing setup is to match up the right size plumbing to the amount of flow you want to run through it. When designing your plumbing setup we personally would not recommend exceeding a velocity over 4 ft/sec. In my experience, you will experience more problems from the higher velocities than by providing the same flow and using additional outlets into the tank and larger sized plumbing acting as feeders to the outlet to keep the velocities under 4 ft/sec.
While not exact, this basically amounts to keeping your flow rates to 3,000 gph when using 2” pipe, 1,500 gph using 1.5” pipe, 700 gph using 1” pipe and 400 gph using ¾” pipe. These are the final flow rates not the pumps rating at 1’ of head. If you try to limit your flow rates to those mentioned, the friction losses you are experiencing should be relatively low. Trying to cram water through the plumbing at higher velocities is typically what causes the higher friction losses.
One problem is thinking that if the pump you are using has a ¾” or 1” inlet or outlet that is the size of plumbing that should be used. Another common misconception that many people have is that 90 degree elbows create an extreme amount of head loss. I’ve heard several people mistakenly quote that you need to count one foot of head loss for every 90 degree elbow in your plumbing setup. The wonderful thing about using these calculations is that you can easily compute the differences in flow under different designs.
What about the head loss calculators that are available on several bulletin boards on the web? One of the biggest weaknesses of the head loss calculators on the internet is that they do not have a wide variety of plumbing fixtures to choose from. In addition they ignore a large number of frictional elements in the plumbing system – e.g., entry and exit, sudden expansion and contraction. Many of them only have an option for the number of feet and flow rate, diameter of pipe and the number of 45 or 90 degree elbows. In addition, with these calculators you still need to guess on the flow rate, and all comparisons to the pump curves to determine the operating point have to be performed manually.
Instructions for Using the Spreadsheet
Attached here as part of the article is a spreadsheet that should make it much simpler for you to calculate head loss. If you are familiar with Excel you should be able to add your own pump curve, but providing detailed instructions on how to add additional pump curves is beyond the scope of this article. On the tab labeled “head loss” you first need to select the pump you are going to calculate the friction loss for. In addition, Reefs.org has just introduced a detailed pump database and the database is accessible from the following URL: http://www.reefs.org/library/pumps. This database contains pump curves, power usage, dimensions, etc. for the majority of the pumps commonly used in the aquarium hobby. Using this article in combination with the database should make pump and plumbing selection much easier than before.
On the tab labeled “head loss” you first need to select the pump you are going to calculate the friction loss for. Once you have selected the pump, you need to enter the diameter (in inches) of the pipe and the total length of pipe to be used. Next, the spreadsheet provides a place to input the number of several different types of valves and fittings that could be used in your setup. It also has a spot to use if you are upsizing or downsizing the pipe at any point in the setup using expansion or reduction couplings. Finally, you will enter the static head of the setup, which is the vertical height that the water would need to be pumped. A closed recirculation loop would have zero static head.
Once all of the information is filled in you need to click the “Solve” button and you should get your answer. The spreadsheet does all of the circular equation solving for you!
One common problem that you might encounter is the fact that the “Solver” is an add-in item in Excel. If you get an error message when trying to use the solver, you will need to install it. On the “Tools” menu in Excel, click on “Add-Ins”, then scroll down until you locate the “Solver Add-In” option. Make sure that you have the box checked. If you don’t have the box checked beside the “Solver Add-In” option then you should be able to simply check the box and then click on “OK” and the Solver Add-In will be installed. Now you should be all set to figure out all sorts of different scenarios.
One limitation that the spreadsheet does have is that currently it will only solve for a problem with one size of pipe. If you are going to use multiple sizes of pipe, your options are to try to manually solve for the equation using both sizes of pipe (the spreadsheet solver won’t work for this), or to try to manipulate the information that you input to give you basically the same answer. One method of solving for multiple sizes of pipe would be to use the friction tables and the head loss calculators found on different websites. You would need to estimate your final flow rate and enter the information on each sized pipe being used into the calculator using your estimated flow rate. When you get your answer concerning friction loss, you would need to add up the friction loss for each size of pipe and compare that to the flow rate you originally used, and see if that matches up to the pump curve. You would need to continue to solve for each pipe size until you got an answer where the same flow rate was used for all sizes of pipe and when the friction and vertical head loss was added together for all sizes of pipe, the total head matched up with the flow rate that you used on the pump’s performance curve. There really isn’t an easy way to solve for friction loss using multiple sizes of pipe, which would explain why the spreadsheet won’t do it!
Conclusions
This article presents an engineering view of plumping and plumbing system design for reef aquariums, and provides a basis for evaluating plumbing designs and selecting pumps. While the mathematics need not be understood by all readers, the key findings based on the mathematics are important for any aquarium system designer: increasing the diameter of the pipe reduces friction and velocity, but not the flow rate. The operating point of the system will occur at the intersection of the system and pump performance curves. Reduce friction by proper sizing of pipes!
In this article we only focused on a single loop design. While the use of multiple branches and splits can be derived from these equations, these will be the subject of a future article.
References
- http://www.mcnallyinstitute.com/
- http://www.pricepump.com/pumpschool/default.htm
- C.R. Liou, “Limitations and Proper Use of the Hazen-Williams Equation”, ASCE vol 124. Journal of Hydraulic Engineering, September 1998.
- Swamee P.K. and Jain,A.K. “Explicit equations for pipe flow problems”, J. of Hydraulics Engineering, ASCE 102(5), pp 657-664, 1976.
- Halland, “Simple and explicit formulas for the friction factor in turbulent pipe flow,” J. Fluids Engineering, 105, pp 89-90, 1983.
- Handbook of Fluid Dynamics, Ed. Richard W. Johnson, CRC Press.
- Fluid Mechanics 2nd Edition, Frank M. White, McGraw Hill Book Company, 1986.

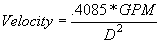
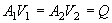
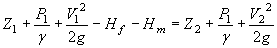
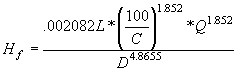
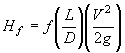
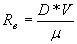
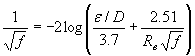
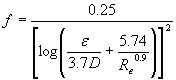
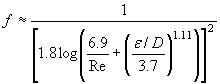
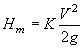


Dear Sanjay – I cannot access the spreadsheet from your hyperlinks. Could you email it to me?