Like the relationship between alkalinity and calcium, the relationship between alkalinity and pH takes many forms. One of the most important of these is simply that alkalinity is defined as the amount of acid necessary to change the pH of the sample to a specific value. Beyond that relationship, however, is where the interesting tidbits lie. How does atmospheric carbon dioxide impact pH in my tank? What is the relationship between alkalinity supplementation and pH? How does the alkalinity impact pH stability in reef tanks? What is a buffer and what does it have to do with alkalinity? This article will endeavor to clarify these relationships.
The Mathematical Relationship Between Carbonate Alkalinity and pH
It turns out that there is an exact mathematical relationship between pH and carbonate alkalinity for any aqueous system in equilibrium with the atmosphere. In this context, carbonate alkalinity is defined as the alkalinity provided by carbonate and bicarbonate, and does not include the minor contributions to alkalinity provided by borate (B(OH)4–), silicate (Si(OH)3O–), phosphate (H2PO4-, HPO4—, and PO4—), hydroxide (OH– and MgOH+) and the negative contribution from protons (H+, HF, and HSO4–). In normal seawater at pH 8.0, the carbonate alkalinity accounts for 96.5% of the total alkalinity, so for most purposes, the contributions from these other ions can be ignored. Two situations where they cannot be ignored, however, are when borate is artificially high, as is true in some commercial salt mixes, and when one is considering
the buffer intensity, where borate is significant even in normal seawater (discussed below).
Carbonate alkalinity (Ac) is mathematically defined as:
1. Ac = [HCO3–] + 2[CO3—]
Where [X] means the concentration of species X. Carbonate (CO3—) is counted twice because it contributes two units of alkalinity for each unit of concentration. The relationship between the amount of bicarbonate and carbonate to pH is well defined if the system is at equilibrium with the atmosphere. Substituting these known relationships into equation 1, we get:
2. Ac = (K1KHPCO2 / [H+]) + 2(K1K2KHPCO2 / [H+]2)
where pCO2 is the concentration CO2 in the air. Current carbon dioxide concentrations are around 350 ppm and have been rising with time, from less than 300 ppm in preindustrial times. KH is the Henry’s law constant for CO2 (which describes the solubility of CO2 in water from the air to form carbonic acid, H2CO3), K1 is the first dissociation constant for H2CO3 (describing the dissociation of H2CO3 to HCO3–), and K2 is the second dissociation constant for H2CO3 (describing the dissociation of HCO3– to CO3—).
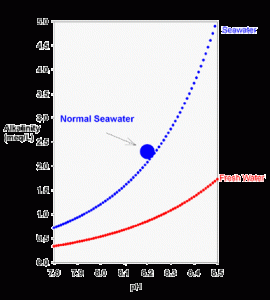
Figure 1. The theoretical relationship between carbonate alkalinity and pH for seawater (blue) and freshwater (red) equilibrated with the atmosphere (350 ppm carbon dioxide) using equations 2 and 3.
It is not easy to look at equation 2 and see any particular relationship between alkalinity and pH, but it is easy to see graphically. Using equations 2 and 3 (the definition of pH), we can plot the relationship graphically (Figure 1).
3. pH = -log [H+]
Note that for purposes of this article, I am ignoring the fact that there are several different pH scales used in seawater that vary on the order of 0.1 to 0.2 pH units, and that activity coefficients are required to properly use such equations. These are fascinating ideas in and of themselves, and may be discussed in detail in future columns, but are unnecessary to understand the fundamental relationship between alkalinity and pH.
There are two things readily apparent from Figure 1. The first is that the alkalinity rises sharply as pH is raised. This becomes especially true above pH 8 in salt water, where there becomes an appreciable concentration of carbonate. Why exactly is this true? Here’s a simple non-quantitative way to think about it:
Carbon dioxide has a specific solubility in water as carbonic acid (H2CO3). Regardless of pH, at a given salt concentration this carbonic acid concentration is always the same. All that determines the concentration of H2CO3 is the amount of CO2 in the air.
Further, at any given pH there is an exact mathematical relationship between H2CO3 and both bicarbonate and carbonate. These relationships are, in fact, those used to derive equation 2 (the first term in equation 2 is bicarbonate, and the second term is carbonate).
For example, at a pH of about 9.3 in freshwater (about 8.4 in seawater) the carbonate concentration is 100 times that of the carbonic acid. At higher pH this multiplier rises, and there is consequently more bicarbonate and carbonate present. More bicarbonate and carbonate results in higher alkalinity, as is shown in Figure 1.
A second interesting feature of Figure 1 is that at any pH, the alkalinity of seawater is much higher than that in fresh water. The reason in simple terms is that the multipliers described above are larger in salt water. The more quantitative reason is that the dissociation constants are higher in salt water. Higher dissociation constants force a higher concentration of bicarbonate and carbonate to be present for a given concentration of carbonic acid. Hence, they result in a higher alkalinity.
A third feature of this relationship involves the pH of seawater as the ambient CO2 level rises. If CO2 is allowed to double (Figure 2), the pH drops by 0.3 pH units (assuming that the alkalinity is unchanged). Consequently, in the future, the pH of seawater may actually drop into the upper 7’s from the 8.0 to 8.2 range present today.
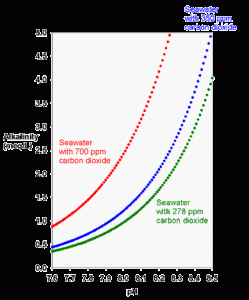
Figure 2. The theoretical relationship between carbonate alkalinity and pH for seawater in equilibrium for preindustrial air (green; 278 ppm carbon dioxide), current air (blue; 350 ppm carbon dioxide) and possible future air (red; 700 ppm carbon dioxide) using equations 2 and 3.
pH vs. Alkalinity in Reef Tanks
At the start of the last section, it was pointed out that “_there is an exact mathematical relationship between pH and carbonate alkalinity for any aqueous system in equilibrium with the atmosphere_”. An important point to keep in mind is that the relationship will be altered slightly if the tank is not in equilibrium with the air. Specifically, reef tanks are often not in equilibrium with the air, making the internal pCO2 for the tank something different than the surrounding air.
For example, tanks using limewater can have a pH value of 8.5 with a total alkalinity of only 3 meq/L. Looking at Figure 2, this puts them off of the theoretical relationship for seawater in ambient air. The fundamental explanation is that the tank is deficient in CO2. In effect, the tank has an internal pCO2 that is more like that for the preindustrial air with 273 ppm CO2 (Figure 2). In this case, driving more CO2 from “normal air” into the water would lower the pH to about 8.2-8.3 while maintaining the same alkalinity.
Likewise, tanks that use calcium carbonate/carbon dioxide reactors often have a pH of 8.0 with an alkalinity of 3 meq/L (or more). Again, that set of values falls off of the theoretical curve shown in Figure 2. In this case, the tank has an artificially high internal pCO2 of more than twice “normal air”. Driving more CO2 from the tank into “normal air” would raise the pH to about 8.2-8.3 while maintaining the same alkalinity.
A third way that reef tanks can present unusual combinations of pH and alkalinity is if the tank is in an environment where the ambient CO2 is far from normal. Rarely would such a situation involve reduced CO2, but homes and businesses are frequently elevated with respect to CO2. Such levels as those represented by the 700-ppm line in Figure 2 are frequently encountered by aquarists, especially those living in newer, “tighter” homes (and some have proven this fact to themselves with carbon dioxide detectors). Aquarists that experience chronic low pH despite adequate alkalinity and aeration may do so because their homes have such elevated levels of carbon dioxide. Many of these aquarists have found that the pH of their tanks rises substantially by simply leaving a window near the tank open to permit better exchange with exterior, “normal” air.
Finally, pCO2 fluctuates within a reef tank every day because of the activities of the organisms present. Some are producing CO2 as a waste product of metabolism, including all organisms in the dark. Those that photosynthesize consume CO2 during the day. As a consequence, the pCO2 rises during the night and declines during the day. This change in pCO2 is largely responsible for the pH fluctuation over the course of a day.
For all of these reasons, a tank may move between the red and green lines of Figure 2 (or further in extreme cases) without the alkalinity changing at all. Typical diurnal pH fluctuations in a reef tank (and in some natural lagoons, for that matter) are about 0.1 to 0.3 pH units. For tanks with a larger fluctuation than about 0.3 pH units, the aquarist might want to look for ways to minimize the fluctuation. This minimization is best accomplished by maximizing the gas exchange between the tank and “normal” air through better circulation, better aeration through devices such as skimmers, having part of the tank system, such as a refugium, on a reverse photocycle so some organisms are always photosynthesizing, or by more rapidly exchanging the room air with exterior air. One can also impact the diurnal pH fluctuation by adding high pH additives (like limewater or other high pH alkalinity additives) during the nightly pH minimum, and by adding low pH additives (like sodium bicarbonate) during the daily pH maximum.
The magnitude of the alkalinity itself, of course, can influence pH stability, and that is the focus of the next section.
What is “Buffering”
Buffer and buffering are terms that are thrown around indiscriminately in the world of reefkeeping, and the actual meaning of these terms is often lost. Many aquarists refer to any alkalinity supplement as a buffer, but this isn’t the case. For example, neither sodium bicarbonate nor sodium carbonate, taken alone, is a true buffer.
A buffer is something that helps minimize pH changes in the presence of added acid or base. No buffer can completely stop the pH from changing when acid or base is added. The change in pH, however, is made smaller when an appropriate buffer is used. A buffer is almost always comprised of two different chemical entities. Bicarbonate and carbonate together, for example, form a buffer in the pH range from about 8 to 11 in seawater, though the buffering is best between about 8.5 and 10.0 (ignoring that at high pH some calcium carbonate may precipitate).
Here’s what is happening on a chemical level. When a base (such as OH–) is added to the system (in an effort to raise pH), some of the bicarbonate is converted to carbonate. This process effectively “uses up” some of the OH– that was added, and the pH does not rise as much as it would without the “buffer”.
4. HCO3– + OH– → CO3—
So overall, we have:
5. HCO3– and CO3— + OH– → less HCO3– and more CO3—
When an acid (H+) is added to the system (in an effort to lower pH), some of the carbonate is converted to bicarbonate. This process effectively “uses up” some of the H+ that was added, and the pH does not drop as much as it would without the “buffer”.
6. CO3— + H+ → HCO3–
So overall we have:
7. HCO3– and CO3— + H+ → more HCO3– and less CO3—
Of course, in order for this process to buffer against both pH rises and pH drops, there must be a significant amount of both HCO3– and CO3— present. At about pH 8.9 in seawater at 25 °C there are equal concentrations of HCO3– and CO3—. At lower pH, there is less CO3—, and at pH 8.0 there is really quite little carbonate in seawater (only about 4% of the bicarbonate level). Consequently, seawater is not especially well buffered against substantial pH drops when the pH is already less than 8.0. It is, however, well buffered against substantial pH rises.
Here’s an actual experiment. Take artificial seawater (Instant Ocean made to S=35; alkalinity measured to be 2.26 meq/L by titration) and add 0.5 meq/L of either acid or base. The results of an immediate pH measurement (before atmospheric carbon dioxide has a chance to equilibrate) are:
Starting Solution pH = 8.10
- 0.5 meq/L OH– added pH = 8.76
- 0.5 meq/L H+ added pH = 6.91
As we can see, the added base (OH–) drives the pH up by only 0.66 units, while the added acid dropped the pH by 1.19 units. This result shows that the water is better buffered against a pH rise than a pH drop, and the reason for this difference is simply that there is more bicarbonate than carbonate at pH 8.1. The only reason that the drop stops at pH 6.9 is that at that point, bicarbonate is really doing the buffering as it is converted into carbonic acid:
8. HCO3– + H+ → H2CO3
The difference in the buffering against substantial pH rises and drops is obvious from such an experiment. Nevertheless, there is much more to fully understanding how a buffer works. Chemists have chosen the term “buffer intensity” (symbolized by b) to reflect the buffering capacity of a solution at any given pH. While it has an exact mathematical definition, it is beyond the scope of this article to describe b in detail. There are, however, a few details worth mentioning in the context of reefkeeping (with additional details are provided in “Aquatic Chemistry Concepts” by James Pankow).
The most important fact to reefkeepers is that the buffering due to bicarbonate and carbonate, at a given pH, is directly related to the carbonate alkalinity. If you double the alkalinity, you double b, and hence have twice as much buffering due to the carbonate and bicarbonate system. In normal seawater, the carbonate/bicarbonate system provides a substantial portion of the total buffering (which is quantified below). Consequently, marine aquaria with higher alkalinity tend to have greater buffering against pH swings.
Other, more esoteric tidbits arise from this system as well. For example, while the buffering against substantial changes can be different in the two different directions (as shown experimentally above), the buffering against very small changes is necessarily exactly the same. That’s what b represents: the buffering against infinitesimally small changes in pH in either direction. b changes as a function of pH, and is maximal when the concentrations of the two forms of the buffer (e.g., bicarbonate and carbonate) are equal. In seawater, b is locally maximized around pH 5.8 where the buffer is H2CO3/HCO3– and at pH 8.9 where the buffer is HCO3–/CO3— (ignoring the fact that other things happen at high pH, like precipitation of magnesium hydroxide and calcium carbonate). These are the points where seawater is most resistant to changes in pH as acid or base is added. Unfortunately, reef tanks are
not usually kept at those pH values, and so the buffering effect of the carbonate system is not as effective at holding pH steady as it might otherwise be.
This lack of effective buffering at a normal tank pH is one of the reasons that some salt manufacturers (Seachem, as told to me by the late Leo Morin, and possibly to a lesser extent, Coralife) boost the borate concentrations in their salt mixes. Since the pKa of borate in seawater is about 8.6, its maximal b (pH 8.6) is not far from the range experienced by reef tanks. In normal seawater at pH 8, borate provides about half of the buffering against a small downward pH change, despite the fact that it provides less than 3% of the total alkalinity. In Seachem salt, where borate is about 10x natural levels, borate totally dominates the buffering in the pH range experienced by reef tanks.
Alkalinity Supplements
One of the most common issues that reefkeepers face involves supplementing alkalinity while maintaining a reasonable pH. Alkalinity supplements impact pH in a variety of ways. One of these ways is the immediate altering of the pH. Different alkalinity supplements have different immediate impacts on pH, as most reefkeepers are aware. This impact is why, for example, limewater needs to be added slowly to a tank but sodium bicarbonate does not.
For this discussion, let’s presume that we want to supplement the carbonate alkalinity of a reef tank. That is, in the end we want to increase the bicarbonate and carbonate levels in the tank. There are a variety of ways to achieve this end, and these different ways have different immediate impacts on pH. Three of these ways (and combinations thereof) are fairly common in reefkeeping. These ways are addition of bicarbonate, carbonate, and hydroxide. In a reef tank that is permitted to equilibrate its total CO2 levels with the atmosphere, these additions all end up with the same final pH. That is, it is only the amount of alkalinity added that determines the final pH, not the nature of the additive itself.
In the short term, however, the impact on pH is very different. To quantify this, I measured to pH change on adding 0.5 meq/L of each of these alkalinity supplements to freshly made salt water (Instant Ocean made to S=35; alkalinity measured to be 2.26 meq/L by titration). Here’s the result for the pH found immediately, and then after 24 and 120 hours of sitting, unstirred, in an open 500- mL beaker:
| Supplement | Initial pH | 24 hour pH | 120 hour pH |
|---|---|---|---|
| none | 8.10 | 8.11 | 8.21 |
| 0.5 meq/L HCO3- | 8.06 | 8.15 | 8.33 |
| 0.5 meq/L CO3– | 8.44 | 8.28 | 8.34 |
| 0.5 meq/L OH- | 8.76 | 8.47 | 8.33 |
| 0.5 meq/L H+ | 6.91 | 7.91 | 8.15 |
From this data it is clear to see the large increase in pH caused by the addition of hydroxide, and also the significant increase when using carbonate. Bicarbonate, on the other hand, shows the expected slight decrease in pH, but not nearly as much as is found with a strong acid of equal concentration. It is also clear that after sufficient time to equilibrate with atmospheric CO2, these differences disappear, and the pH is the same for all of the 0.5-meq/L alkalinity additions. This is an important result: in seawater in equilibrium with the atmosphere, for a given alkalinity there is a single pH that results, regardless of what was added to get to that alkalinity.
Here’s how to think of these additions. When these chemicals are added to the water, there is a change in the relative concentrations of carbonate and bicarbonate, and it is the ratio of these two ions that determines the pH.
Hydroxide Addition
For hydroxide addition, the first thing that happens is that bicarbonate is converted into carbonate:
9. HCO3– + OH– → CO3—
and the small amount of carbonic acid present is converted into bicarbonate:
10. H2CO3 + OH– → HCO3– + H2O
The net effect is that the pH rise that is normally encountered by adding hydroxide to water is reduced. For example, adding 0.5 meq/L of hydroxide to freshwater would drive the pH into the 10’s. In seawater, the pH rises much less, and the conversion of bicarbonate to carbonate is largely responsible.
In this situation, the tank is now deficient in H2CO3 (because the small equilibrium amount of H2CO3 normally present was partially converted to bicarbonate by the OH– addition), and the tank proceeds to absorb CO2 from the air, bringing the pH back down a bit by releasing H+. There are many ways to show these reactions, but the net process involves CO2 from the air becoming carbonic acid, the carbonic acid deprotonating to bicarbonate, and some of the bicarbonate deprotonating to carbonate:
11. CO2 (atmosphere) + H2O → H2CO3
12. H2CO3 → HCO3– + H+
13. HCO3– → CO3— + H+
The reactions taking place in equations 11-13 all serve to lower the pH (from 8.76 to 8.33 in the experiment above). When equilibrium is reached, however, the pH has not dropped all of the way back to the point before the hydroxide was added, but is slightly elevated (8.33 in the example above). When all is said and done, and the tank has fully equilibrated with the air, the hydroxide addition has caused the tank to experience an increase in bicarbonate and carbonate, and in pH.
Carbonate Addition
The case for carbonate addition is similar to that for hydroxide. In this situation, the pH rises because much of the carbonate combines with H+ to form bicarbonate. This obviously reduces the H+, which results in a higher pH:
14. H+ + CO3— (added) → HCO3–
In this case, the net short-term effect is that carbonate and bicarbonate increase, and the pH rises (from 8.10 to 8.44 in the experiment above). In the long term, the higher pH causes more CO2 to be pulled in from the air, as was the case with hydroxide additions. This limits the pH rise, and further increases the bicarbonate concentration. Still, the end effect is the same as hydroxide addition: the tank experiences an increase in bicarbonate and carbonate, and in pH.
Bicarbonate Addition
The addition of bicarbonate as an alkalinity supplement is rather different. In this case, the bicarbonate partially dissociates into carbonate and H+, and the tank experiences an increase in bicarbonate and carbonate, and a drop in pH.:
15. HCO3– → H+ + CO3—
Consequently, the immediate effect on pH is for it to drop. The drop is small because not much of the bicarbonate dissociates at normal tank pH, but enough does to drive the pH a bit lower (from 8.10 to 8.06 in the experiment above).
In the long term, however, the effect is different. Since a substantial amount of bicarbonate was added and the pH did not change much, the tank is now overloaded with bicarbonate with respect to what it would normally have in equilibrium with air. Some of the bicarbonate picks up a proton, becomes carbonic acid, and the pH rises as the CO2 is blown off to the atmosphere:
16. HCO3– + H+ → H2CO3 → CO2 + H2O
In the experiment above, this effect has caused the pH to rise from 8.06 to 8.33. So the long-term effect of bicarbonate addition (as it is for any addition to carbonate alkalinity) is to raise pH even though the short-term effect was to lower it.
Summary
Alkalinity and pH are two of what I would call the big 5 in terms of parameters important in keeping a reef tank (the others being calcium, salinity, and temperature). Alkalinity and pH are related to each other in ways that are obvious, and in other ways that are much more subtle. Unfortunately, these parameters are often problematic for people maintaining aquaria, and the relationship between the two is one of the biggest areas of concern. I have found that more than half of the questions posed on reef chemistry internet forums relate to pH or alkalinity. Obviously, these parameters are confusing to many aquarists. Hopefully, this article has put these relationships in perspective, and will help aquarists to better understand their systems.
Two texts that provide additional detail on this subject are shown below. Millero’s book is especially suited to seawater, but isn’t as detailed or mathematical as Pankow’s.
- Millero, Frank J.; Editor. Chemical Oceanography, Second Edition. (1996), 496 pp.
- Pankow, James F.; Aquatic Chemistry Concepts (1991), 673 pp.


0 Comments
Trackbacks/Pingbacks